Identify Counting Numbers and Whole Numbers

In the following exercises, determine which of the following numbers are a) counting numbers and b) whole numbers.

1. $0,\frac{2}{3},5,8.1,125$

   $\mathrm{}$

2. $0,\frac{4}{9},3.9,50,221$

   $\mathrm{}$

Model Whole Numbers

In the following exercises, use place value notation to find the value of the number modeled by the base -10 blocks.

3. 

    

4. 

Identify the Place Value of a Digit

In the following exercises, find the place value of the given digits.

5. [latex]579,601[/latex]
   • [latex]9[/latex]
   • [latex]6[/latex]
   • [latex]0[/latex]
   • [latex]7[/latex]
   • [latex]5[/latex]
6. [latex]56,804,379[/latex]
   • [latex]8[/latex]
   • [latex]6[/latex]
   • [latex]4[/latex]
   • [latex]7[/latex]
   • [latex]0[/latex]

Use Place Value to Name Whole Numbers

In the following exercises, name each number in words.

7. [latex]1,078[/latex]
8. [latex]364,510[/latex]
9. [latex]5,846,103[/latex]
10. [latex]37,889,005[/latex]
11. The height of Mount Rainier is [latex]14,410[/latex] feet.
12. Seventy years is [latex]613,200[/latex] hours.
13. One year is [latex]525,600[/latex] minutes.
14. The U.S. Census estimate of the population of Miami-Dade county was [latex]2,617,176[/latex].
15. The population of Chicago was [latex]2,718,782[/latex].
16. There are projected to be [latex]23,867,000[/latex] college and university students in the US in five years.
17. About twelve years ago there were [latex]20,665,415[/latex] registered automobiles in California.
18. The population of China is expected to reach [latex]1,377,583,156[/latex] in [latex]2016[/latex].
19. The population of India is estimated at [latex]1,267,401,849[/latex] as of July [latex]1, 2014[/latex].

Use Place Value to Write Whole Numbers

In the following exercises, write each number as a whole number using digits.

20. four hundred twelve
21. two hundred fifty-three
22. thirty-five thousand, nine hundred seventy-five
23. sixty-one thousand, four hundred fifteen
24. eleven million, forty-four thousand, one hundred sixty-seven
25. eighteen million, one hundred two thousand, seven hundred eighty-three
26. three billion, two hundred twenty-six million, five hundred twelve thousand, seventeen
27. eleven billion, four hundred seventy-one million, thirty-six thousand, one hundred six
28. The population of the world was estimated to be seven billion, one hundred seventy-three million people.
29. The age of the solar system is estimated to be four billion, five hundred sixty-eight million years.
30. Lake Tahoe has a capacity of thirty-nine trillion gallons of water.
31. The federal government budget was three trillion, five hundred billion dollars.

Round Whole Numbers

In the following exercises, round to the indicated place value.

Round to the nearest ten:

32. [latex]386[/latex]
33. [latex]2,931[/latex]

Round to the nearest ten:

34. [latex]792[/latex]
35. [latex]5,647[/latex]

Round to the nearest hundred:

36. [latex]13,748[/latex]
37. [latex]391,794[/latex]

Round to the nearest hundred:

38. [latex]28,166[/latex]
39. [latex]481,628[/latex]

Round to the nearest ten:

40. [latex]1,492[/latex]
41. [latex]1,497[/latex]

Round to the nearest thousand:

42. [latex]2,391[/latex]
43. [latex]2,795[/latex]

Round to the nearest hundred:

44. [latex]63,994[/latex]
45. [latex]63,949[/latex]

Round to the nearest thousand:

46. [latex]163,584[/latex]
47. [latex]163,246[/latex]

Adding Whole Numbers

Use Addition Notation

In the following exercises, translate the following from math expressions to words.

48. [latex]5+25[/latex]
49. [latex]6+36[/latex]
50. [latex]13+18[/latex]
51. [latex]15+16[/latex]
52. [latex]214+642[/latex]
53. [latex]438+113[/latex]

Model Addition of Whole Numbers

In the following exercises, model the addition.

54. [latex]2+4[/latex]
55. [latex]5+3[/latex]
56. [latex]8+4[/latex]
57. [latex]5+9[/latex]
58. [latex]14+75[/latex]
59. [latex]15+63[/latex]
60. [latex]16+25[/latex]
61. [latex]14+27[/latex]

Add Whole Numbers

In the following exercises, fill in the missing values in each chart.

Exercise 1

Exercise 2

Exercises 3

 

Exercise 4

Exercise 5

 

Exercise 6

Add Whole Numbers

In the following exercises, add.

62. [latex]0+13[/latex]
63. [latex]13+0[/latex]
64. [latex]0+5,280[/latex]
65. [latex]5,280+0[/latex]
66. [latex]8+3[/latex]
67. [latex]3+8[/latex]
68. [latex]7+5[/latex]
69. [latex]5+7[/latex]
70. [latex]45+33[/latex]
71. [latex]37+22[/latex]
72. [latex]71+28[/latex]
73. [latex]43+53[/latex]
74. [latex]26+59[/latex]
75. [latex]38+17[/latex]
76. [latex]64+78[/latex]
77. [latex]92+39[/latex]
78. [latex]168+325[/latex]
79. [latex]247+149[/latex]
80. [latex]584+277[/latex]
81. [latex]175+648[/latex]
82. [latex]832+199[/latex]
83. [latex]775+369[/latex]
84. [latex]6,358+492[/latex]
85. [latex]9,184+578[/latex]
86. [latex]3,740+18,593[/latex]
87. [latex]6,118+15,990[/latex]
88. [latex]485,012+619,848[/latex]
89. [latex]368,911+857,289[/latex]
90. [latex]24,731+592+3,868[/latex]
91. [latex]28,925+817+4,593[/latex]
92. [latex]8,015+76,946+16,570[/latex]
93. [latex]6,291+54,107+28,635[/latex]

Translate Word Phrases to Math Notation

In the following exercises, translate each phrase into math notation and then simplify.

94. the sum of [latex]13[/latex] and [latex]18[/latex]
95. the sum of [latex]12[/latex] and [latex]19[/latex]
96. the sum of [latex]90[/latex] and [latex]65[/latex]
97. the sum of [latex]70[/latex] and [latex]38[/latex]
98. [latex]33[/latex] increased by [latex]49[/latex]
99. [latex]68[/latex] increased by [latex]25[/latex]

100. [latex]250[/latex] more than [latex]599[/latex]
101. [latex]115[/latex] more than [latex]286[/latex]

102. the total of [latex]628[/latex] and [latex]77[/latex]
103. the total of [latex]593[/latex] and [latex]79[/latex]
104. [latex]1,482[/latex] added to [latex]915[/latex]
105. [latex]2,719[/latex] added to [latex]682[/latex]

Add Whole Numbers in Applications

In the following exercises, solve the problem.

Home remodeling

Sophia remodeled her kitchen and bought a new range, microwave, and dishwasher. The range cost [latex]$1,100[/latex], the microwave cost [latex]$250[/latex], and the dishwasher cost [latex]$525[/latex]

. What was the total cost of these three appliances?

Sports equipment

Aiden bought a baseball bat, helmet, and glove. The bat cost [latex]$299[/latex]

, the helmet cost [latex]$35[/latex], and the glove cost [latex]$68[/latex]. What was the total cost of Aiden’s sports equipment?

Bike riding

Ethan rode his bike [latex]14[/latex] miles on Monday, [latex]19[/latex]

miles on Tuesday, [latex]12[/latex] miles on Wednesday, [latex]25[/latex] miles on Friday, and [latex]68[/latex] miles on Saturday. What was the total number of miles Ethan rode?

Business

Chloe has a flower shop. Last week she made [latex]19[/latex]

floral arrangements on Monday, [latex]12[/latex] on Tuesday, [latex]23[/latex] on Wednesday, [latex]29[/latex] on Thursday, and [latex]44[/latex] on Friday. What was the total number of floral arrangements Chloe made?

Apartment size

Jackson lives in a [latex]7[/latex] room apartment. The number of square feet in each room is [latex]238,120,156,196,100,132,[/latex] and [latex]225[/latex]. What is the total number of square feet in all [latex]7[/latex] rooms?

Weight

Seven men rented a fishing boat. The weights of the men were [latex]175,192,148,169,205,181[/latex], and [latex]225[/latex] pounds. What was the total weight of the seven men?

Salary

Last year Natalie’s salary was [latex]$82,572[/latex]. Two years ago, her salary was [latex]$79,316[/latex], and three years ago it was [latex]$75,298[/latex]. What is the total amount of Natalie’s salary for the past three years?

Home sales

Emma is a realtor. Last month, she sold three houses. The selling prices of the houses were [latex]$292,540[/latex], [latex]$505,875[/latex], and [latex]$423,699[/latex]. What was the total of the three selling prices?

Finding Perimeter

In the following exercises, find the perimeter of each figure.

Exercise 1

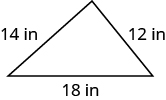
Exercise 2

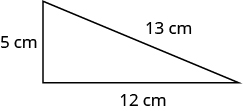
Exercise 3

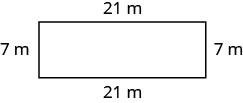
Exercise 4

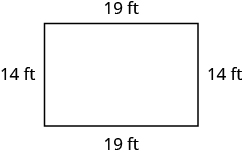
Exercise 5

 

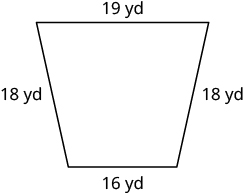
Exercise 6

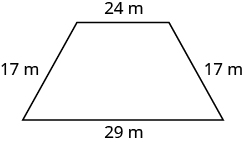
Exercise 7

 

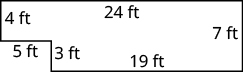
Exercise 8

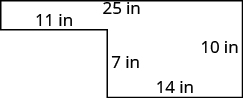
Subtracting Whole Numbers

Use Subtraction Notation

In the following exercises, translate from math notation to words.

106. [latex]15−9[/latex]
107. [latex]18−16[/latex]

108. [latex]42−35[/latex]
109. [latex]83−64[/latex]
110. [latex]675−350[/latex]
111. [latex]790−525[/latex]

Model Subtraction of Whole Numbers

In the following exercises, model the subtraction.

112. [latex]5−2[/latex]
113. [latex]8−4[/latex]
114. [latex]6−3[/latex]
115. [latex]7−5[/latex]
116. [latex]18−5[/latex]
117. [latex]19−8[/latex]
118. [latex]17−8[/latex]
119. [latex]17−9[/latex]
120. [latex]35−13[/latex]
121. [latex]32−11[/latex]
122. [latex]61−47[/latex]
123. [latex]55−36[/latex]

Subtract Whole Numbers

In the following exercises, subtract and then check by adding.

124. [latex]9−4[/latex]
125. [latex]9−3[/latex]
126. [latex]8−0[/latex]
127. [latex]2−0[/latex]
128. [latex]38−16[/latex]
129. [latex]45−21[/latex]
130. [latex]85−52[/latex]
131. [latex]99−47[/latex]
132. [latex]493−370[/latex]
133. [latex]268−106[/latex]
134. [latex]5,946−4,625[/latex]
135. [latex]7,775−3,251[/latex]
136. [latex]75−47[/latex]
137. [latex]63−59[/latex]
138. [latex]461−239[/latex]
139. [latex]486−257[/latex]
140. [latex]525−179[/latex]
141. [latex]542−288[/latex]
142. [latex]6,318−2,799[/latex]
143. [latex]8,153−3,978[/latex]
144. [latex]2,150−964[/latex]
145. [latex]4,245−899[/latex]
146. [latex]43,650−8,982[/latex]
147. [latex]35,162−7,885[/latex]

Translate Word Phrases to Algebraic Expressions

In the following exercises, translate and simplify.

148. The difference of [latex]10[/latex] and [latex]3[/latex]
149. The difference of [latex]12[/latex] and [latex]8[/latex]
150. The difference of [latex]15[/latex] and [latex]4[/latex]

151. The difference of [latex]18[/latex] and [latex]7[/latex]
152. Subtract [latex]6[/latex] from [latex]9[/latex]
153. Subtract [latex]8[/latex] from [latex]9[/latex]
154. Subtract [latex]28[/latex] from [latex]75[/latex]
155. Subtract [latex]59[/latex] from [latex]81[/latex]
156. [latex]45[/latex] decreased by [latex]20[/latex]
157. [latex]37[/latex] decreased by [latex]24[/latex]

158. [latex]92[/latex] decreased by [latex]67[/latex]
159. [latex]75[/latex] decreased by [latex]49[/latex]

160. [latex]12[/latex] less than [latex]16[/latex]
161. [latex]15[/latex] less than [latex]19[/latex]

162. [latex]38[/latex] less than [latex]61[/latex]
163. [latex]47[/latex] less than [latex]62[/latex]

Mixed Practice

In the following exercises, simplify.

164. [latex]76−47[/latex]
165. [latex]91−53[/latex]
166. [latex]256−184[/latex]
167. [latex]305−262[/latex]
168. [latex]719+341[/latex]
169. [latex]647+528[/latex]
170. [latex]2,015−1,993[/latex]
171. [latex]2,020−1,984[/latex]

In the following exercises, translate and simplify.

172. Seventy more than thirty-five
173. Sixty more than ninety-three
174. [latex]13[/latex] less than [latex]41[/latex]
175. [latex]28[/latex] less than [latex]36[/latex]
176. The difference of [latex]100[/latex] and [latex]76[/latex]
177. The difference of [latex]1,000[/latex] and [latex]945[/latex]

Subtract Whole Numbers in Applications

In the following exercises, solve.

Temperature

The high temperature on June [latex]2[/latex] in Las Vegas was [latex]80[/latex] degrees and the low temperature was [latex]63[/latex] degrees. What was the difference between the high and low temperatures?

Temperature

The high temperature on June [latex]1[/latex] in Phoenix was [latex]97[/latex] degrees and the low was [latex]73[/latex] degrees. What was the difference between the high and low temperatures?

Class size

Olivia’s third grade class has [latex]35[/latex] children. Last year, her second grade class had [latex]22[/latex] children. What is the difference between the number of children in Olivia’s third grade class and her second grade class?

Class size

There are [latex]82[/latex] students in the school band and [latex]46[/latex] in the school orchestra. What is the difference between the number of students in the band and the orchestra?

Shopping

A mountain bike is on sale for [latex]$399[/latex]. Its regular price is [latex]$650[/latex]. What is the difference between the regular price and the sale price?

Shopping

A mattress set is on sale for [latex]$755[/latex]. Its regular price is [latex]$1,600[/latex]. What is the difference between the regular price and the sale price?

Savings

John wants to buy a laptop that costs [latex]$840[/latex]. He has [latex]$685[/latex] in his savings account. How much more does he need to save in order to buy the laptop?

Banking

Mason had [latex]$1,125[/latex] in his checking account. He spent [latex]$892[/latex]. How much money does he have left?

Multiplying Whole Numbers

Use Multiplication Notation

In the following exercises, translate from math notation to words.

178. [latex]4×7[/latex]
179. [latex]8×6[/latex]
180. [latex]5⋅12[/latex]
181. [latex]3⋅9[/latex]
182. [latex](10)(25)[/latex]
183. [latex](20)(15)[/latex]
184. [latex]42(33)[/latex]
185. [latex]39(64)[/latex]

Model Multiplication of Whole Numbers

In the following exercises, model the multiplication.

186. [latex]3×6[/latex]
187. [latex]4×5[/latex]
188. [latex]5×9[/latex]
189. [latex]3×9[/latex]

Multiply Whole Numbers

In the following exercises, fill in the missing values in each chart.

Exercise 1

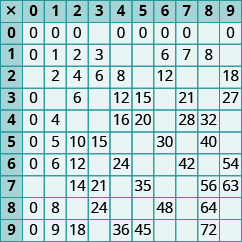
Exercise 2

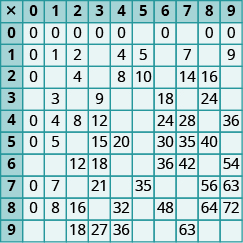
Exercise 3

Exercise 4

Exercise 5

Exercise 6

Exercise 7

Exercise 8

Multiply Whole Numbers

In the following exercises, multiply.

190. [latex]0⋅15[/latex]
191. [latex]0⋅41[/latex]
192. [latex](99)0[/latex]
193. [latex](77)0[/latex]
194. [latex]1⋅43[/latex]
195. [latex]1⋅34[/latex]
196. [latex](28)1[/latex]
197. [latex](65)1[/latex]
198. [latex]1(240,055)[/latex]
199. [latex]1(189,206)[/latex]
200. [latex]7⋅6[/latex]
201. [latex]6⋅7[/latex]
202. [latex]8×9[/latex]
203. [latex]9×8[/latex]
204. [latex](79)(5)[/latex]
205. [latex](58)(4)[/latex]
206. [latex]275⋅6[/latex]
207. [latex]638⋅5[/latex]
208. [latex]3,421×7[/latex]
209. [latex]9,143×3[/latex]
210. [latex]52(38)[/la37(45)
211. [latex]96⋅73[/latex]
212. [latex]89⋅56[/latex]
213. [latex]27×85[/latex]
214. [latex]53×98[/latex]
215. [latex]23⋅10[/latex]
216. [latex]19⋅10[/latex]
217. [latex](100)(36)[/latex]
218. [latex](100)(25)[/latex]
219. [latex]1,000(88)[/latex]
220. [latex]1,000(46)[/latex]
221. [latex]50×1,000,000[/latex]
222. [latex]30×1,000,000[/latex]
223. [latex]247×139[/latex]
224. [latex]156×328[/latex]
225. [latex]586(721)[/latex]
226. [latex]472(855)[/latex]
227. [latex]915⋅879[/latex]
228. [latex]968⋅926[/latex]
229. [latex](104)(256)[/latex]
230. [latex](103)(497)[/latex]
231. [latex]348(705)[/latex]
232. [latex]485(602)[/latex]
233. [latex]2,719×543[/latex]
234. [latex]3,581×724[/latex]

Translate Word Phrases to Math Notation

In the following exercises, translate and simplify.

235. the product of [latex]18[/latex] and [latex]33[/latex]
236. the product of [latex]15[/latex] and [latex]22[/latex]
237. fifty-one times sixty-seven
238. forty-eight times seventy-one
239. twice [latex]249[/latex]
240. twice [latex]589[/latex]
241. ten times three hundred seventy-five
242. ten times two hundred fifty-five

Mixed Practice, Part I

In the following exercises, simplify.

243. [latex]38×37[/latex]
244. [latex]86×29[/latex]
245. [latex]415−267[/latex]
246. [latex]341−285[/latex]
247. [latex]6,251+4,749[/latex]
248. [latex]3,816+8,184[/latex]
249. [latex](56)(204)[/latex]
250. [latex](77)(801)[/latex]
251. [latex]947⋅0[/latex]
252. [latex]947+0[/latex]
253. [latex]15,382+1[/latex]
254. [latex]15,382⋅1[/latex]

Mixed Practice, Part II

In the following exercises, translate and simplify.

255. the difference of [latex]50[/latex] and [latex]18[/latex]
256. the difference of [latex]90[/latex] and [latex]66[/latex]
257. twice [latex]35[/latex]
258. twice [latex]140[/latex]
259. [latex]20[/latex] more than [latex]980[/latex]
260. [latex]65[/latex] more than [latex]325[/latex]
261. the product of [latex]12[/latex] and [latex]875[/latex]
262. the product of [latex]15[/latex] and [latex]905[/latex]
263. subtract [latex]74[/latex] from [latex]89[/latex]
264. subtract [latex]45[/latex] from [latex]99[/latex]
265. the sum of [latex]3,075[/latex] and [latex]95[/latex]
266. the sum of [latex]6,308[/latex] and [latex]724[/latex]
267. [latex]366[/latex] less than [latex]814[/latex]
268. [latex]388[/latex] less than [latex]925[/latex]

Multiply Whole Numbers in Applications

In the following exercises, solve.

Party supplies

Tim brought [latex]9[/latex] six-packs of soda to a club party. How many cans of soda did Tim bring?

Sewing

Kanisha is making a quilt. She bought [latex]6[/latex] cards of buttons. Each card had four buttons on it. How many buttons did Kanisha buy?

Field trip

Seven school busses let off their students in front of a museum in Washington, DC. Each school bus had [latex]44[/latex] students. How many students were there?

Gardening

Kathryn bought [latex]8[/latex] flats of impatiens for her flower bed. Each flat has [latex]24[/latex] flowers. How many flowers did Kathryn buy?

Charity

Rey donated [latex]15[/latex] twelve-packs of t-shirts to a homeless shelter. How many t-shirts did he donate?

School

There are [latex]28[/latex] classrooms at Anna C. Scott elementary school. Each classroom has [latex]26[/latex] student desks. What is the total number of student desks?

Recipe

Stephanie is making punch for a party. The recipe calls for twice as much fruit juice as club soda. If she uses [latex]10[/latex] cups of club soda, how much fruit juice should she use?

Gardening

Hiroko is putting in a vegetable garden. He wants to have twice as many lettuce plants as tomato plants. If he buys [latex]12[/latex] tomato plants, how many lettuce plants should he get?

Government

The United States Senate has twice as many senators as there are states in the United States. There are [latex]50[/latex] states. How many senators are there in the United States Senate?

Recipe

Andrea is making potato salad for a buffet luncheon. The recipe says the number of servings of potato salad will be twice the number of pounds of potatoes. If she buys [latex]30[/latex] pounds of potatoes, how many servings of potato salad will there be?

Painting

Jane is painting one wall of her living room. The wall is rectangular, [latex]13[/latex] feet wide by [latex]9[/latex] feet high. What is the area of the wall?

Home décor

Shawnte bought a rug for the hall of her apartment. The rug is [latex]3[/latex] feet wide by [latex]18[/latex] feet long. What is the area of the rug?

Room size

The meeting room in a senior center is rectangular, with length [latex]42[/latex] feet and width [latex]34[/latex] feet. What is the area of the meeting room?

Gardening

June has a vegetable garden in her yard. The garden is rectangular, with length [latex]23[/latex] feet and width [latex]28[/latex] feet. What is the area of the garden?

NCAA basketball

According to NCAA regulations, the dimensions of a rectangular basketball court must be [latex]94[/latex] feet by [latex]50[/latex] feet. What is the area of the basketball court?

NCAA football

According to NCAA regulations, the dimensions of a rectangular football field must be [latex]360[/latex] feet by [latex]160[/latex] feet. What is the area of the football field?

Dividing Whole Numbers

Use Division Notation

In the following exercises, translate from math notation to words.

269. [latex]54÷9[/latex]
270. $\frac{56}{7}$
271. $\frac{32}{8}$
272. $6\stackrel{¯<!--\; ¯\; -->}{)42}$
273. [latex]48÷6[/latex]
274. $\frac{63}{9}$
275. $7\stackrel{¯<!--\; ¯\; -->}{)63}$
276. [latex]72÷8[/latex]

Model Division of Whole Numbers

In the following exercises, model the division.

277. [latex]15÷5[/latex]
278. [latex]10÷5[/latex]
279. $\frac{14}{7}$
280. $\frac{18}{6}$
281. $4\stackrel{¯<!--\; ¯\; -->}{)20}$
282. $3\stackrel{¯<!--\; ¯\; -->}{)15}$
283. [latex]24÷6[/latex]
284. [latex]16÷4[/latex]

Divide Whole Numbers

In the following exercises, divide. Then check by multiplying.

285. [latex]18÷2[/latex]
286. [latex]14÷2[/latex]
287. $\frac{27}{3}$

288. $\frac{30}{3}$
289. $4\stackrel{¯<!--\; ¯\; -->}{)28}$
290. $4\stackrel{¯<!--\; ¯\; -->}{)36}$
291. $\frac{45}{5}$
292. $\frac{35}{5}$
293. [latex]72/8[/latex]
294. $8\stackrel{¯<!--\; ¯\; -->}{)64}$
295. $\frac{35}{7}$
296. [latex]42÷7[/latex]
297. $15\stackrel{¯<!--\; ¯\; -->}{)15}$
298. $12\stackrel{¯<!--\; ¯\; -->}{)12}$
299. [latex]43÷43[/latex]
300. [latex]37÷37[/latex]
301. $\frac{23}{1}$
302. $\frac{29}{1}$
303. [latex]19÷1[/latex]
304. [latex]17÷1[/latex]
305. [latex]0÷4[/latex]
306. [latex]0÷8[/latex]
307. [latex]\frac{5}{0}[/latex]
308. $\frac{9}{0}$
309. $\frac{26}{0}$
310. $\frac{32}{0}$
311. $12\stackrel{¯<!--\; ¯\; -->}{)0}$
312. $16\stackrel{¯<!--\; ¯\; -->}{)0}$
313. [latex]72÷3[/latex]
314. [latex]57÷3[/latex]
315. $\frac{96}{8}$
316. $\frac{78}{6}$
317. $5\stackrel{¯<!--\; ¯\; -->}{)465}$
318. $4\stackrel{¯<!--\; ¯\; -->}{)528}$
319. [latex]924÷7[/latex]
320. [latex]861÷7[/latex]
321. $\frac{5,226}{6}$
322. [latex]3,7768[/latex]
323. $4\stackrel{¯<!--\; ¯\; -->}{)31,324}$
324.  
325. [latex]7,209÷3[/latex]
326. [latex]4,806÷3[/latex]
327. [latex]5,406÷6[/latex]
328. [latex]3,208÷4[/latex]
329. $4\stackrel{¯<!--\; ¯\; -->}{)2,816}$
330. $6\stackrel{¯<!--\; ¯\; -->}{)3,624}$
331. [latex]91,8819[/latex]
332. [latex]83,2568[/latex]
333. [latex]2,470÷7[/latex]
334. [latex]3,741÷7[/latex]
335. $8\stackrel{}{)55,305}$

     $\stackrel{}{¯<!--\; ¯\; -->}$

336. $9\stackrel{¯<!--\; ¯\; -->}{)51,492}$
337. [latex]431,1745[/latex]
338. [latex]297,2774[/latex]
339. [latex]130,016÷3[/latex]
340. [latex]105,609÷2[/latex]
341. $15\stackrel{¯<!--\; ¯\; -->}{)5,735}$
342. $\frac{4,933}{21}$
343. [latex]56,883÷67[/latex]
344. [latex]43,725/75[/latex]
345. $\frac{30,144}{314}$
346. [latex]26,145÷415[/latex]
347. $273\stackrel{¯<!--\; ¯\; -->}{)542,195}$
348. [latex]816,243÷462[/latex]

Mixed Practice

In the following exercises, simplify.

349. [latex]15(204)[/latex]
350. [latex]74⋅391[/latex]
351. [latex]256−184[/latex]
352. [latex]305−262[/latex]
353. [latex]719+341[/latex]
354. [latex]647+528[/latex]
355. $25\stackrel{¯<!--\; ¯\; -->}{)875}$
356. [latex]1104÷23[/latex]

Translate Word Phrases to Algebraic Expressions

In the following exercises, translate and simplify.

357. the quotient of [latex]45[/latex] and [latex]15[/latex]
358. the quotient of [latex]64[/latex] and [latex]16[/latex]
359. the quotient of [latex]288[/latex] and [latex]24[/latex]
360. the quotient of [latex]256[/latex] and [latex]32[/latex]

Divide Whole Numbers in Applications

In the following exercises, solve.

Trail mix

Ric bought [latex]6[/latex]4 ounces of trail mix. He wants to divide it into small bags, with [latex]2[/latex] ounces of trail mix in each bag. How many bags can Ric fill?

Crackers

Evie bought a [latex]42[/latex] ounce box of crackers. She wants to divide it into bags with [latex]3[/latex] ounces of crackers in each bag. How many bags can Evie fill?

Astronomy class

There are [latex]125[/latex] students in an astronomy class. The professor assigns them into groups of [latex]5[/latex]. How many groups of students are there?

Flower shop

Melissa’s flower shop got a shipment of [latex]152[/latex] roses. She wants to make bouquets of [latex]8[/latex] roses each. How many bouquets can Melissa make?

Baking

One roll of plastic wrap is [latex]48[/latex] feet long. Marta uses [latex]3[/latex] feet of plastic wrap to wrap each cake she bakes. How many cakes can she wrap from one roll?

Dental floss

One package of dental floss is [latex]54[/latex] feet long. Brian uses [latex]2[/latex] feet of dental floss every day. How many days will one package of dental floss last Brian?

Mixed Practice (Applications)

In the following exercises, solve.

Miles per gallon

Susana’s hybrid car gets [latex]45[/latex] miles per gallon. Her son’s truck gets [latex]17[/latex] miles per gallon. What is the difference in miles per gallon between Susana’s car and her son’s truck?

Distance

Mayra lives [latex]53[/latex] miles from her mother’s house and [latex]71[/latex] miles from her mother-in-law’s house. How much farther is Mayra from her mother-in-law’s house than from her mother’s house?

Field trip

The 45 students in a Geology class will go on a field trip, using the college’s vans. Each van can hold 9 students. How many vans will they need for the field trip?

Potting soil

Aki bought a [latex]128[/latex] ounce bag of potting soil. How many [latex]4[/latex] ounce pots can he fill from the bag?

Hiking

Bill hiked [latex]8[/latex] miles on the first day of his backpacking trip, [latex]14[/latex] miles the second day, [latex]11[/latex] miles the third day, and [latex]17[/latex] miles the fourth day. What is the total number of miles Bill hiked?

Reading

Last night Emily read [latex]6[/latex] pages in her Business textbook, [latex]26[/latex] pages in her History text, [latex]15[/latex] pages in her Psychology text, and [latex]9[/latex] pages in her math text. What is the total number of pages Emily read?

Patients

LaVonne treats [latex]12[/latex] patients each day in her dental office. Last week she worked [latex]4[/latex] days. How many patients did she treat last week?

Scouts

There are [latex]14[/latex] boys in Dave’s scout troop. At summer camp, each boy earned [latex]5[/latex] merit badges. What was the total number of merit badges earned by Dave’s scout troop at summer camp?