Volume and Surface Area: Fresh Take

Lumen Learning

Volume and Surface Area: Fresh Take

Find the volume of a rectangular solid, sphere, cylinder, and cone
Find the surface area of a rectangular solid, sphere, and cylinder

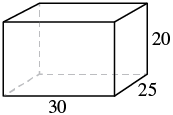
Finding the Volume and Surface Area of Rectangular Solids

The Main Idea

The volume of a rectangular solid is a measurement that tells us how much space is enclosed or occupied by the solid in three dimensions. It helps us understand the capacity or quantity of material that can fit within the shape. Since volume is a measure of three-dimensional space, the units will be in cubic units.

To calculate the volume of a rectangular solid, we multiply its three dimensions: length, width, and height. The formula for finding the volume is [latex]V = L × W × H[/latex], where [latex]V[/latex] represents the volume, [latex]L[/latex] represents the length, [latex]W[/latex] represents the width, and [latex]H[/latex] represents the height. This can also be written as [latex]V = B × H[/latex], where [latex]B[/latex] is the area of the base – [latex]B = L × W[/latex].

The surface area of a rectangular solid is a measurement that tells us the total area of all the exposed surfaces of the solid. It helps us understand the amount of material needed to cover the shape. Since surface area is a measure of two-dimensional space, the units will be in square units.

To calculate the surface area of a rectangular solid, we add up the areas of all its faces. For a rectangular solid, there are six faces: the top, bottom, front, back, left side, and right side. Each face is a rectangle, so we can find the area of each face by multiplying its length and width. Finally, we sum up the areas of all the faces to find the total surface area. The formula for finding the surface area of a rectangular solid is [latex]SA = 2LW + 2LH + 2WH[/latex], where [latex]SA[/latex] represents the surface area, [latex]L[/latex] represents the length, [latex]W[/latex] represents the width, and [latex]H[/latex] represents the height of the rectangular solid.

A rectangular crate has a length of [latex]30[/latex] inches, width of [latex]25[/latex] inches, and height of [latex]20[/latex] inches. Find its:

volume
surface area

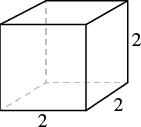
Finding the Volume and Surface Area of a Cube

The Main Idea

A cube is a three-dimensional shape with equal sides, forming six identical square faces.

To find the volume of a cube, you raise the length of one side to the power of three. The formula for calculating the volume of a cube is [latex]V = s^3[/latex], where [latex]V[/latex] represents the volume and [latex]s[/latex] represents the length of one side.

The surface area of a cube is the sum of the areas of all its faces. Since all the faces are squares with equal sides, you can multiply the length of one side by itself and then multiply by six to account for all the faces. The formula for finding the surface area of a cube is [latex]SA = 6s^2[/latex], where [latex]SA[/latex] represents the surface area and [latex]s[/latex] represents the length of one side.

A notepad cube measures [latex]2[/latex] inches on each side. Find its:

volume
surface area

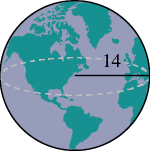
Finding the Volume and Surface Area of a Sphere

The Main Idea

A sphere is a three-dimensional shape with all points equidistant from its center. To find the volume of a sphere, you use the formula [latex]V = (4/3)πr^3[/latex], where [latex]V[/latex] represents the volume and [latex]r[/latex] represents the radius of the sphere. The radius is the distance from the center of the sphere to any point on its surface. The surface area of a sphere is the total area covered by its outer surface. You can calculate it using the formula [latex]SA = 4πr^2[/latex], where [latex]SA[/latex] represents the surface area and [latex]r[/latex] represents the radius of the sphere.

A globe of Earth is in the shape of a sphere with radius [latex]14[/latex] centimeters. Find its:

volume
surface area

Round the answer to the nearest hundredth.

The following video shows an example of how to find the surface area of a sphere.

You can view the transcript for “Find the Surface Area of a Sphere” here (opens in new window).

In the next video we show an example of how to find the volume of a sphere given it’s diameter.

You can view the transcript for “Ex: Volume of a Sphere” here (opens in new window).

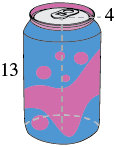
Finding the Volume and Surface Area of a Cylinder

The Main Idea

A cylinder is a three-dimensional shape with two circular bases and a curved surface connecting the bases.

To find the volume of a cylinder, you multiply the area of the base (which is a circle) by the height of the cylinder. The formula for calculating the volume of a cylinder is [latex]V = πr^2h[/latex], where [latex]V[/latex] represents the volume, [latex]r[/latex] represents the radius of the base, and [latex]h[/latex] represents the height of the cylinder.

The surface area of a cylinder is the sum of the areas of its curved surface and the two circular bases. The formula for finding the surface area of a cylinder is [latex]SA = 2πrh + 2πr^2[/latex], where [latex]SA[/latex] represents the surface area, [latex]r[/latex] represents the radius of the base, and [latex]h[/latex] represents the height of the cylinder.

The radius of the base of a soda can is [latex]4[/latex] centimeters and the height is [latex]13[/latex] centimeters. Assume the can is shaped exactly like a cylinder.
Find its:

volume
surface area

Round the answer to the nearest hundredth.

The following video shows an example of how to find the volume of a cylinder.

You can view the transcript for “Ex: Volume of a Cylinder” here (opens in new window).

In the next example video we show how to find the surface area of a cylinder.

You can view the transcript for “Find the surface Area of a Cylinder” here (opens in new window).

Finding the Volume of a Cone

The Main Idea

A cone is a three-dimensional shape with a circular base and a pointed top.

To find the volume of a cone, you multiply the area of the base (which is a circle) by the height of the cone and divide by [latex]3[/latex]. The formula for calculating the volume of a cone is [latex]V = \frac{1}{3}πr^2h[/latex], where [latex]V[/latex] represents the volume, [latex]r[/latex] represents the radius of the base, and [latex]h[/latex] represents the height of the cone.

Marty’s favorite pub serves french fries in a paper wrap shaped like a cone. What is the volume of a conic wrap that is [latex]8[/latex] inches tall and [latex]5[/latex] inches in diameter? Round the answer to the nearest hundredth.

In the following video we provide another example of how to find the volume of a cone.

You can view the transcript for “Ex: Determine Volume of a Cone” here (opens in new window).

Step 2. Identify what you are looking for.	the volume of the crate
Step 3. Name. Choose a variable to represent it.	let [latex]V[/latex] = volume
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]V=LWH[/latex] [latex]V=30\cdot 25\cdot 20[/latex]
Step 5. Solve the equation.	[latex]V=15,000[/latex]
Step 6. Check: Double check your math.
Step 7. Answer the question.	The volume is [latex]15,000[/latex] cubic inches.

Step 2. Identify what you are looking for.	the surface area of the crate
Step 3. Name. Choose a variable to represent it.	let [latex]S[/latex] = surface area
Step 4. Translate. Write the appropriate formula. Substitute.	[latex]S=2LH+2LW+2WH[/latex] [latex]S=2\left(30\cdot 20\right)+2\left(30\cdot 25\right)+2\left(25\cdot 20\right)[/latex]
Step 5. Solve the equation.	[latex]S=3,700[/latex]
Step 6. Check: Check it yourself!
Step 7. Answer the question.	The surface area is [latex]3,700[/latex] square inches.

1.
Step 2. Identify what you are looking for.	the volume of the cube
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula.	[latex]V={s}^{3}[/latex]
Step 5. Solve the equation.	[latex]V={2}^{3}[/latex] [latex]V=8[/latex]
Step 6. Check: Check that you did the calculations correctly.
Step 7. Answer the question.	The volume is [latex]8[/latex] cubic inches.

2.
Step 2. Identify what you are looking for.	the surface area of the cube
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula.	[latex]S=6{s}^{2}[/latex]
Step 5. Solve the equation.	[latex]S=6\cdot {2}^{2}[/latex] [latex]S=24[/latex]
Step 6. Check: The check is left to you.
Step 7. Answer the question.	The surface area is [latex]24[/latex] square inches.

Step 2. Identify what you are looking for.	the volume of the sphere
Step 3. Name. Choose a variable to represent it.	let [latex]V[/latex] = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex] )	[latex]V=\Large\frac{4}{3}\normalsize\pi {r}^{3}[/latex] [latex]V\approx \Large\frac{4}{3}\normalsize\left(3.14\right){14}^{3}[/latex]
Step 5. Solve.	[latex]V\approx 11,488.21[/latex]
Step 6. Check: We leave it to you to check your calculations.
Step 7. Answer the question.	The volume is approximately [latex]11,488.21[/latex] cubic inches.

Step 2. Identify what you are looking for.	the surface area of the sphere
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula. Substitute. (Use 3.14 for [latex]\pi[/latex] )	[latex]S=4\pi {r}^{2}[/latex] [latex]S\approx 4\left(3.14\right){14}^{2}[/latex]
Step 5. Solve.	[latex]S\approx 2461.76[/latex]
Step 6. Check: We leave it to you to check your calculations.
Step 7. Answer the question.	The surface area is approximately [latex]2461.76[/latex] square inches.

Step 2. Identify what you are looking for.	the volume of the cylinder
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use [latex]3.14[/latex] for [latex]\pi[/latex] )	[latex]V=\pi {r}^{2}h[/latex] [latex]V\approx \left(3.14\right){4}^{2}\cdot 13[/latex]
Step 5. Solve.	[latex]V\approx 653.12[/latex]
Step 6. Check: We leave it to you to check.
Step 7. Answer the question.	The volume is approximately [latex]653.12[/latex] cubic centimeters.

Step 2. Identify what you are looking for.	the surface area of the cylinder
Step 3. Name. Choose a variable to represent it.	let S = surface area
Step 4. Translate. Write the appropriate formula. Substitute. (Use [latex]3.14[/latex] for [latex]\pi[/latex] )	[latex]S=2\pi {r}^{2}+2\pi rh[/latex] [latex]S\approx 2\left(3.14\right){4}^{2}+2\left(3.14\right)\left(4\right)13[/latex]
Step 5. Solve.	[latex]S\approx 427.04[/latex]
Step 6. Check: We leave it to you to check your calculations.
Step 7. Answer the question.	The surface area is approximately [latex]427.04[/latex] square centimeters.

Step 1. Read the problem. Draw the figure and label it with the given information. Notice here that the base is the circle at the top of the cone.
Step 2. Identify what you are looking for.	the volume of the cone
Step 3. Name. Choose a variable to represent it.	let V = volume
Step 4. Translate. Write the appropriate formula. Substitute. (Use [latex]3.14[/latex] for [latex]\pi[/latex] , and notice that we were given the distance across the circle, which is its diameter. The radius is [latex]2.5[/latex] inches.)	[latex]V=\Large\frac{1}{3}\normalsize\pi {r}^{2}h[/latex] [latex]V\approx \Large\frac{1}{3}\normalsize 3.14{\left(2.5\right)}^{2}\left(8\right)[/latex]
Step 5. Solve.	[latex]V\approx 52.33[/latex]
Step 6. Check: We leave it to you to check your calculations.
Step 7. Answer the question.	The volume of the wrap is approximately [latex]52.33[/latex] cubic inches.