- Classify triangles based on their angles and side lengths
- Determine the measure of the third angle in a triangle when the measures of two angles are given
- Apply properties of similar triangles to find unknown side lengths
- Use the Pythagorean theorem to calculate unknown side lengths in triangles
Types of Triangles
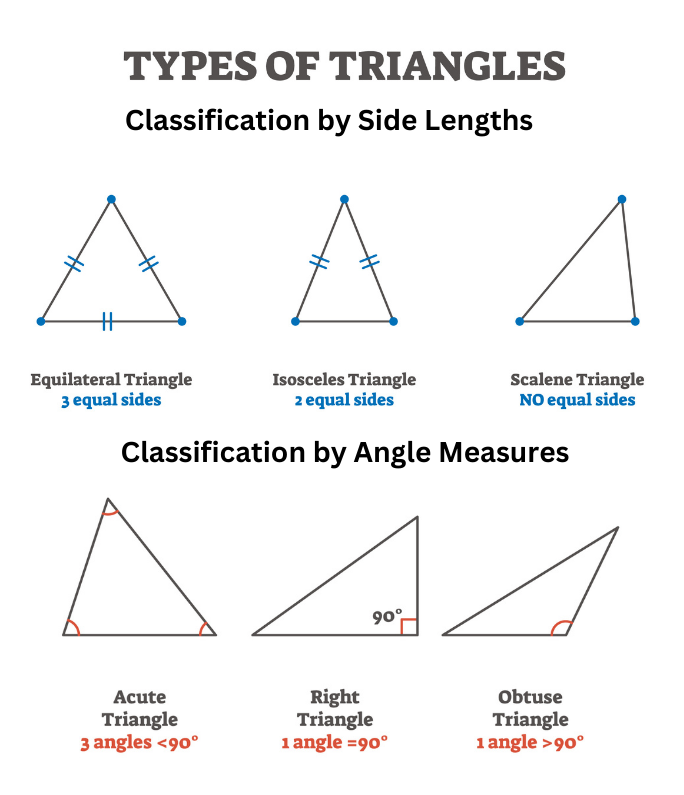
In geometry, triangles are one of the fundamental shapes. They can be classified based on their angle measures and side lengths, which helps us categorize and understand different types of triangles.
triangle classifications
- Classification by Side Lengths:
- Equilateral Triangle: An equilateral triangle has all three sides of equal length. Consequently, all three angles are also equal, measuring [latex]60[/latex] degrees each.
- Isosceles Triangle: An isosceles triangle has two sides of equal length. This means two of its angles are also equal.
- Scalene Triangle: A scalene triangle has no sides of equal length. Consequently, all three angles are different from one another.
- Classification by Angle Measures:
- Right Triangle: A right triangle has one angle measuring exactly [latex]90[/latex] degrees.
- Acute Triangle: An acute triangle has all three angles measuring less than [latex]90[/latex] degrees.
- Obtuse Triangle: An obtuse triangle has one angle measuring greater than [latex]90[/latex] degrees.