- Understand the concepts of sets, including empty sets, subsets, and proper subsets, and use correct set notation
- Describe and perform set operations (union, intersection, complement, and difference) using proper set notation
- Create and interpret Venn diagrams to represent and analyze set relationships and operations
- Apply the concepts of sets, subsets, and cardinality properties to solve real-life problems
Sets
The Main Idea
A set is a collection of unique objects or elements. These elements can be anything: numbers, people, other sets, etc. For example, the set [latex]A[/latex] could be the set of all positive integers, while the set B could be the set of all colors in the rainbow.
The empty set, also known as the null set, is a special set that contains no elements. For example, the set of all dogs with six legs is an empty set, since no such dogs exist.
Notation
In set theory, we often use curly brackets – [latex]\{\}[/latex] – to denote a set. An example of a set is [latex]A = \{a, b, c, d\}[/latex].
Commonly, we will use a variable to represent a set, to make it easier to refer to that set later. We usually denote sets with capital letters such as [latex]A[/latex], [latex]B[/latex], [latex]C[/latex], etc.
The symbol [latex]\in[/latex] means “is an element of”.
An empty set is denoted by the symbols is notated by [latex]\emptyset[/latex] or [latex]\{ \}[/latex].
You can view the transcript for “Sets Basics – Introduction | Don’t Memorise” here (opens in new window).
You can view the transcript for “Sets – Listing Method | Don’t Memorise” here (opens in new window).
Subsets
The Main Idea
A set [latex]A[/latex] is said to be a subset of another set [latex]B[/latex] if every element in [latex]A[/latex] is also in [latex]B[/latex]. We denote this by [latex]A \subseteq B[/latex]. For instance, if [latex]B = \{\text{red}, \text{green}, \text{blue}, \text{yellow}\}[/latex] and [latex]A = \{\text{red}, \text{blue}, \text{yellow}\}[/latex], then [latex]A[/latex] is a subset of [latex]B[/latex] because every color in [latex]A[/latex] is also in [latex]B[/latex].
A proper subset is similar to a subset, but with one key difference: if [latex]A[/latex] is a proper subset of [latex]B[/latex], then there is at least one element in [latex]B[/latex] that is not in [latex]A[/latex]. We denote this by [latex]A \subset B[/latex]. If [latex]B = \{\text{red}, \text{green}, \text{blue}, \text{yellow}\}[/latex] and [latex]A = \{\text{red}, \text{blue}\}[/latex], then [latex]A[/latex] is a proper subset of [latex]B[/latex].
To calculate the number of subsets and proper subsets in a set you must use the following formulas:
If you have [latex]n[/latex] elements in your set:
- Number of subsets: [latex]2^{n}[/latex]
- Number of proper subsets: [latex]2^{n}−1[/latex]
[latex]A[/latex] = the set of all even numbers
[latex]B = \{2, 4, 6\}[/latex]
[latex]C = \{2, 3, 4, 6\}[/latex]
Here [latex]B \subset A[/latex] since every element of [latex]B[/latex] is also an even number, so is an element of [latex]A[/latex]. More formally, we could say [latex]B \subset A[/latex] since if [latex]x \in B[/latex], then [latex]x \in A[/latex]. It is also true that [latex]B \subset C[/latex]. [latex]C[/latex] is not a subset of [latex]A[/latex], since [latex]C[/latex] contains an element, [latex]3[/latex], that is not contained in [latex]A[/latex].
[latex]X = \{1, 3, 7, 5\}[/latex]
[latex]Y = \{1, 3 \}[/latex]
[latex]Z = \{1, m, n, 3, 5\}[/latex]
You can view the transcript for “What is a Subset? | Don’t Memorise” here (opens in new window).
You can view the transcript for “Subsets, Proper Subsets and Supersets | Don’t Memorise” here (opens in new window).
You can view the transcript for “What is a Null Set | Is Null Set a Subset of Every Set? | Don’t Memorise” here (opens in new window).
Set Operations: Union, Intersection, Complement, and Difference
A big part of understanding proper notation in sets and set operations is being able to read and translate the symbols used. There are a lot of different symbols used that make things confusing. We can use the following table as a reminder of what each symbol means:
| Symbol | Symbol Meaning | Translation |
|---|---|---|
| [latex]\in[/latex] | “is an element of” or “is an element in” | [latex]1 \in P[/latex] reads as: [latex]1[/latex] is an element of the set [latex]P[/latex] |
| [latex]\subseteq[/latex] | Subset | [latex]C \subseteq R[/latex] reads as: set [latex]C[/latex] is a subset of set [latex]R[/latex] |
| [latex]\subset[/latex] | Proper Subset | [latex]C \subset R[/latex] reads as: set [latex]C[/latex] is a proper subset of set [latex]R[/latex] |
| [latex]\cup[/latex] | Union of two sets | [latex]C \cup R[/latex] reads as: the union of sets [latex]C[/latex] and [latex]R[/latex] |
| [latex]\cap[/latex] | Intersection of two sets | [latex]C \cap R[/latex] reads as: the intersection of sets [latex]C[/latex] and [latex]R[/latex] |
| [latex]R'[/latex], or [latex]R^c[/latex], or ~[latex]R[/latex] | Complement of a set | [latex]R'[/latex] reads as: the complement of set [latex]R[/latex] |
| [latex]\setminus[/latex] | Difference of two sets | [latex]C \setminus R[/latex] reads as: the difference between sets [latex]C[/latex] and [latex]R[/latex] |
Now that we can see what each symbol translates to let’s break down each of the formal notations of the set operations to better understand what they are stating.
Union
The Main Idea
The union of two sets contains all the elements contained in either set (or both sets) and is notated [latex]A \cup B[/latex]. The formal notation states, [latex]x \in A \cup B[/latex] if [latex]x \in A[/latex] or [latex]x \in B[/latex] (or both).
If we break this down and translate the symbols into words it is easier to understand.
- [latex]x \in A \cup B[/latex] reads as “[latex]x[/latex] is an element of the union of sets [latex]A[/latex] and [latex]B[/latex] “
- [latex]x \in A[/latex] reads as “[latex]x[/latex] is an element of set [latex]A[/latex] “
- [latex]x \in B[/latex] reads as “[latex]x[/latex] is an element of set [latex]B[/latex] “
If we add all the parts we translated into words back into the original formal definition it reads as “[latex]x[/latex] is an element of the union of sets [latex]A[/latex] and [latex]B[/latex] if [latex]x[/latex] is an element of set [latex]A[/latex] or [latex]x[/latex] is an element of set [latex]B[/latex] (or both).”
Intersection
The Main Idea
The intersection of two sets contains only the elements that are in both sets. The intersection is notated [latex]A \cap B[/latex]. More formally, [latex]x \in A \cap B[/latex] if [latex]x \in A[/latex] and [latex]x \in B[/latex].
If we break this down and translate the symbols into words it is easier to understand.
- [latex]x \in A \cap B[/latex] reads as “[latex]x[/latex] is an element of the intersection of sets [latex]A[/latex] and [latex]B[/latex] “
- [latex]x \in A[/latex] reads as “[latex]x[/latex] is an element of set [latex]A[/latex] “
- [latex]x \in B[/latex] reads as “[latex]x[/latex] is an element of set [latex]B[/latex] “
If we add all the parts we translated into words back into the original formal definition it reads as “[latex]x[/latex] is an element of the intersection of sets [latex]A[/latex] and [latex]B[/latex] if [latex]x[/latex] is an element of set [latex]A[/latex] and [latex]x[/latex] is an element of set [latex]B[/latex]. “
intersection and union symbols
The intersection [latex]\cup[/latex] and union [latex]\cap[/latex] symbols look a little like letters in the alphabet. In fact, that’s a trick for remembering them.
The union symbol looks like a capital U, for union.
The intersection symbol looks a little like a big lower-case n, for in-tersect.
Difference
The Main Idea
The difference of two sets is the list of all the elements that are in one set but not present in the other. The difference between two sets is notated [latex]A \setminus B[/latex].
More formally, [latex]x \in A \setminus B[/latex] if [latex]x \in A[/latex] & [latex]x \notin B[/latex].
If we break this down and translate the symbols into words it is easier to understand.
- [latex]x \in A \setminus B[/latex] reads as “[latex]x[/latex] is an element of the difference of sets [latex]A[/latex] and [latex]B[/latex] “
- [latex]x \in A[/latex] reads as “[latex]x[/latex] is an element of set [latex]A[/latex] “
- [latex]x \notin B[/latex] reads as “[latex]x[/latex] is not an element of set [latex]B[/latex] “
If we add all the parts we translated into words back into the original formal definition it reads as “[latex]x[/latex] is an element of the difference of sets [latex]A[/latex] and [latex]B[/latex] if [latex]x[/latex] is an element of set [latex]A[/latex] and [latex]x[/latex] is not an element of set [latex]B[/latex] .“
Universal Set
The Main Idea
A universal set is a set that contains all the elements we are interested in. This would have to be defined by the context.
- If we were discussing searching for books, the universal set might be all the books in the library.
- If we were grouping your Facebook friends, the universal set would be all your Facebook friends.
- If you were working with sets of numbers, the universal set might be all whole numbers, all integers, or all real numbers.
Complement
The Main Idea
A complement is relative to the universal set. The complement of a set [latex]A[/latex] contains everything that is not in the universal set [latex]A[/latex]. The complement is notated [latex]A'[/latex], or [latex]A^c[/latex], or sometimes ~[latex]A[/latex].
[latex]A = \{\text{red, green, blue}\}[/latex]
[latex]B = \{\text{red, yellow, orange}\}[/latex]
[latex]C = \{\text{red, orange, yellow, green, blue, purple}\}[/latex] Find the following:
- Find [latex]A \cup C[/latex]
- Find [latex]B^c \cap A[/latex]
You can view the transcript for “Sets: Union, Intersection, Complement” here (opens in new window).
Any of the set operations can be grouped together or stand alone to make statements about different sets. When symbols are grouped together they form an order of operations. Don’t forget, like in arithmetic, when applying the order of operations parenthesis indicates the operation you do first.
- Find [latex](H \cap F) \cup W[/latex]
- Find [latex](F \cup W) \cap H[/latex]
- Find [latex](H \cap F)^c \cap W[/latex]
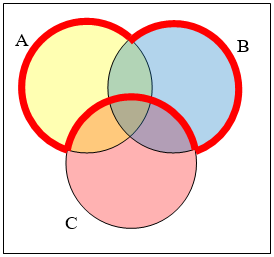
Venn Diagrams
The Main Idea
Venn diagrams are a helpful tool for visualizing the relationships between sets and performing set operations. A Venn diagram uses overlapping circles or other shapes to illustrate the logical relationships between two or more sets of items. Each circle represents a set, with the items of the set represented by points within the circle. Here’s how you can create and interpret Venn diagrams for various set relationships and operations:
- Representing Sets: In a Venn diagram, each set is represented by a circle. For example, if you have two sets A and B, you can represent them with two circles. The universal set is often represented by a rectangle encompassing all the circles.
- Union: The union of two sets A and B (A ∪ B) is represented by the area covered by both circles A and B, including the overlap.
- Intersection: The intersection of two sets A and B (A ∩ B) is represented by the area where the two circles overlap.
- Difference: The difference of two sets A and B (A – B) is represented by the area that is in circle A but not in circle B.
- Complement: The complement of a set A (A’) is represented by the area that is outside circle A but within the universal set.
- Empty Set: An empty set or null set, which contains no elements, can be represented by a circle with nothing in it. If the set is a subset of another set, it can be represented by a circle within the larger set, but with no elements.
You can view the transcript for “Sets: drawing a Venn diagram” here (opens in new window).
You can view the transcript for “Venn Diagrams” here (opens in new window).
Cardinality
Cardinality is a fundamental concept in set theory and refers to the number of elements in a set. It is a measure of the “size” of a set. Remember, cardinality is just a fancy way of saying how many elements are in a set. The cardinality of a set is denoted by [latex]{\lvert}A{\rvert}[/latex], where [latex]A[/latex] is the set. For example, if you have a set [latex]A = \{1, 2, 3, 4, 5\}[/latex], the cardinality of set [latex]A[/latex] is [latex]5[/latex], written as [latex]{\lvert}A{\rvert} = 5[/latex].
Cardinality Properties
- Union of Sets: The cardinality of the union of two sets A and B can be found using the formula:
[latex]n(A \cup B) = n(A) + n(B) – n(A \cap B)[/latex]
- Complement of a Set: The cardinality of a set A can also be found by subtracting the number of elements not in A (the complement of A, represented as [latex]\bar{A}[/latex]) from the total number of elements in the universal set U. This is expressed in the formula:
[latex]n(A) = n(U) – n(A)[/latex]
Notice that the first property can also be written in an equivalent form by solving for the cardinality of the intersection:
[latex]n(A \cap B) = n(A) + n(B) – n(A \cup B)[/latex]
It might be easier to understand the cardinality properties if we break them down into words.
| Union | [latex]\begin{array}{lc} n(A \cup B) = \\ n(A) + n(B) - n(A \cap B) \end{array}[/latex] |
the cardinality of the union of set [latex]A[/latex] with set [latex]B[/latex] will consists of the cardinality of [latex]A[/latex] together with the cardinality of [latex]B[/latex], after deducting the cardinality of their intersection. |
| Intersection | [latex]\begin{array}{lc} n(A \cap B) = \\ n(A) + n(B) - n(A \cap B) \end{array}[/latex] |
the cardinality of the intersection of set [latex]A[/latex] with set [latex]B[/latex] will consists of the cardinality of [latex]A[/latex] together with the cardinality of [latex]B[/latex], after deducting the cardinality of their union. |
| Complement | [latex]n(A) = n(U) - n(A)[/latex] | the cardinality of the complement of [latex]A[/latex] will consist of the cardinality of the universal set less the cardinality of [latex]A[/latex]. In other words, it’s the cardinality of all the elements that are not in [latex]A[/latex] |
Let’s try some more examples dealing with the cardinality properties.
- [latex]43[/latex] believed in UFOs
- [latex]25[/latex] believed in Bigfoot
- [latex]8[/latex] believed in ghosts and Bigfoot
- [latex]2[/latex] believed in all three
- [latex]44[/latex] believed in ghosts
- [latex]10[/latex] believed in UFOs and ghosts
- [latex]5[/latex] believed in UFOs and Bigfoot
How many people surveyed believed in at least one of these things?
You can view the transcript for “Properties of the cardinality of the set” here (opens in new window).
