Set Theory

1. List out the elements of the set “The letters of the word Mississipi”
2. List out the elements of the set “Months of the year”
3. Write a verbal description of the set {[latex]3,6,9[/latex]}
4. Write a verbal description of the set {a,i,e,o,u}
5. Is {[latex]1,3,5[/latex]} a subset of the set of odd integers?
6. Is {A,B,C} a subset of the set of letters of the alphabet?

For problems [latex]7-12[/latex], consider the sets below, and indicate if each statement is true or false.

7. [latex]3[/latex]∈B
8. [latex]5[/latex]∈C
9. B⊂A
10. C⊂A
11. C⊂B
12. C⊂U

Using the sets from above, and treating U as the Universal set, find each of the following:

13. Using the sets from above, and treating U as the Universal set, find each of the following:
14. A∪B
15. A∪C
16. A∩C
17. B∩C
18. Ac
19. Bc

Let [latex]D={b,a,c,k}[/latex], [latex]E={t,a,s,k}[/latex], [latex]F={b,a,t,h}[/latex]. Using these sets, find the following:

19. Dc∩E
20. Fc∩D
21. (D∩E)∪F
22. D∩(E∪P)
23. (F∩E)c∩D
24. (D∪E)c∩F

Create a Venn diagram to illustrate each of the following:

25. (F∩E)∪D
26. (D∪E)c∩F
27. (Fc∩E′)∩D
28. (D∪E)∪Fw

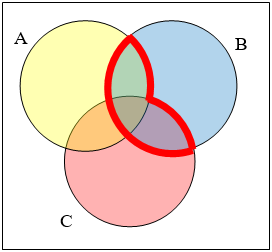
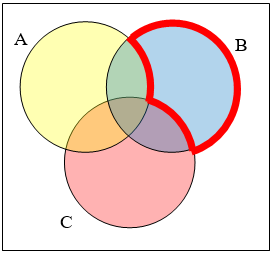
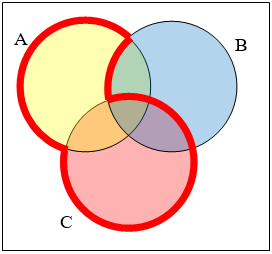
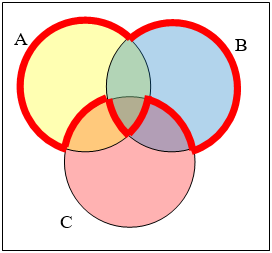
Write an expression for the shaded region.

29. 
30. 
31. 
32. 

Let A = {[latex]1,2,3,4,5[/latex]} B = {[latex]1,3,5[/latex]} C = {[latex]4,6[/latex]}. Find the cardinality of the given set.

33. n(A)
34. n(B)
35. n(A∪C)
36. n(A∩C)

The Venn diagram here shows the cardinality of each set. Use this in [latex]37-40[/latex] to find the cardinality of given set.

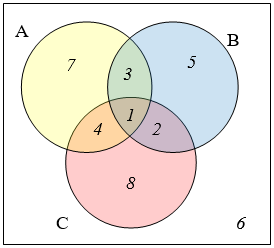
37. n(A∩C)
38. n(B∪C)
39. n(A∩B∩C2)
40. n(A∩Bc∩C)
41. If n(G) = [latex]20[/latex],n(H) = [latex]30[/latex],n(G ∩ H) = [latex]5[/latex], find n(G ∪ H)
42. If n(G) = [latex]5[/latex],n(H) = [latex]8[/latex],n(G ∩ H) = [latex]4[/latex], find n(G ∪ H)
43. A survey was given asking whether they watch movies at home from Netflix, Redbox, or a video store. Use the results to determine how many people use Redbox.

[latex]52[/latex] only use Netflix
[latex]62[/latex] only use Redbox
[latex]24[/latex] only use a video store
[latex]16[/latex] use only a video store and Redbox
[latex]48[/latex] use only Netflix and Redbox
[latex]30[/latex] use only a video store and Netflix
[latex]10[/latex] use all three
[latex]25[/latex] use none of these

44. A survey asked buyers whether color, size, or brand influenced their choice of cell phone. The results are below. How many people were influenced by brand?

[latex]5[/latex] only said color
[latex]8[/latex] only said size
[latex]16[/latex] only said brand
[latex]20[/latex] said only color and size
[latex]42[/latex] said only color and brand
[latex]53[/latex] said only size and brand
[latex]102[/latex] said all three
[latex]20[/latex] said none of these

45. Use the given information to complete a Venn diagram, then determine: a) how many students have seen exactly one of these movies, and b) how many had seen only Star Wars.

[latex]18[/latex] had seen The Matrix (M)
[latex]24[/latex] had seen Star Wars (SW)
[latex]20[/latex] had seen Lord of the Rings (LotR)
[latex]10[/latex] had seen M and SW
[latex]14[/latex] had seen LotR and SW
[latex]12[/latex] had seen M and LotR
[latex]6[/latex] had seen all three

46. A survey asked people what alternative transportation modes they use. Using the data to complete a Venn diagram, then determine: a) what percent of people only ride the bus, and b) how many people don’t use any alternate transportation.

[latex]30\%[/latex] use the bus
[latex]20\%[/latex] ride a bicycle
[latex]25\%[/latex] walk
[latex]5\%[/latex] use the bus and ride a bicycle
[latex]10\%[/latex] ride a bicycle and walk
[latex]12\%[/latex] use the bus and walk
[latex]2\%[/latex] use all three

Logic

For questions [latex]47-48[/latex], list the set of integers that satisfy the given conditions.

47. A positive multiple of [latex]5[/latex] and not a multiple of [latex]2[/latex]
48. Greater than [latex]12[/latex] and less than or equal to [latex]18[/latex]

For questions [latex]49-50[/latex], write the negation of each quantified statement.

49. Everyone failed the quiz today.
50. Someone in the car needs to use the restroom.

51. Translate each statement from symbolic notation into English sentences. Let A represent “Elvis is alive” and let G represent “Elvis gained weight”.
    1. A∨G
    2. ∼(A∧G)
    3. G→∼A
    4. A↔∼G

For questions [latex]52-55[/latex], create a truth table for each statement.

52. A∧∼B
53. ∼(∼A∨B)
54. A∧B)→C
55. A∨B)→∼C

Questions [latex]56-59[/latex]:
In this lesson, we have been studying the inclusive or, which allows both A and B to be true. The exclusive or does not allow both to be true; it translates to “either A or B, but not both.”

56. For each situation, decide whether the “or” is most likely exclusive or inclusive.
    1. An entrée at a restaurant includes soup or a salad.
    2. You should bring an umbrella or a raincoat with you.
    3. We can keep driving on I-[latex]5[/latex] or get on I-[latex]405[/latex] at the next exit.
    4. You should save this document on your computer or a flash drive.
57. Complete the truth table for the exclusive or.

    $\begin{array}{|ccc|}\hline A& B& A\vee <!--\; \vee \; -->B\\ \mathrm{T}& \mathrm{T}& \\ \mathrm{T}& \mathrm{F}& \\ \mathrm{F}& \mathrm{T}& \\ \mathrm{F}& \mathrm{F}& \\ \hline\end{array}$

58. Complete the truth table for (A∨B)∧∼(A∧B)

    $\begin{array}{|cccccc|}\hline A& B& A\vee <!--\; \vee \; -->B& A\wedge <!--\; \wedge \; -->B& \sim <!--\; \sim \; -->(A\wedge <!--\; \wedge \; -->B)& (A\vee <!--\; \vee \; -->B)\wedge <!--\; \wedge \; -->\sim <!--\; \sim \; -->(A\wedge <!--\; \wedge \; -->B)\\ \mathrm{T}& \mathrm{T}& & & & \\ \mathrm{T}& \mathrm{F}& & & & \\ \mathrm{F}& \mathrm{T}& & & & \\ \mathrm{F}& \mathrm{F}& & & & \\ \hline\end{array}$

59. Compare your answers for questions 56 and 57. Can you explain the similarities?
60. Consider the statement “If you are under age [latex]17[/latex], then you cannot attend this movie.”
    1. Write the converse.
    2. Write the inverse.
    3. Write the contrapositive.
61. Assume that the statement “If you swear, then you will get your mouth washed out with soap” is true. Which of the following statements must also be true?
    1. If you don’t swear, then you won’t get your mouth washed out with soap.
    2. If you don’t get your mouth washed out with soap, then you didn’t swear.
    3. If you get your mouth washed out with soap, then you swore.

For questions [latex]62-64[/latex], write the negation of each conditional statement.

62. If you don’t look both ways before crossing the street, then you will get hit by a car.
63. If Luke faces Vader, then Obi-Wan cannot interfere.
64. If you weren’t talking, then you wouldn’t have missed the instructions.
65. Assume that the biconditional statement “You will play in the game if and only if you attend all practices this week” is true. Which of the following situations could happen?
    1. You attended all practices this week and didn’t play in the game.
    2. You didn’t attend all practices this week and played in the game.
    3. You didn’t attend all practices this week and didn’t play in the game.

For questions [latex]66-67[/latex], use De Morgan’s Laws to rewrite each conjunction as a disjunction, or each disjunction as a conjunction.

66. It is not true that Tina likes Sprite or [latex]7[/latex]-Up.
67. It is not the case that you need a dated receipt and your credit card to return this item.

For questions [latex]68-73[/latex], use a Venn diagram or truth table or common form of an argument to decide whether each argument is valid or invalid.

68. If a person is on this reality show, they must be self-absorbed. Laura is not self-absorbed. Therefore, Laura cannot be on this reality show.
69. If you are a triathlete, then you have outstanding endurance. LeBron James is not a triathlete. Therefore, LeBron does not have outstanding endurance.
70. Jamie must scrub the toilets or hose down the garbage cans. Jamie refuses to scrub the toilets. Therefore, Jamie will hose down the garbage cans.
71. Some of these kids are rude. Jimmy is one of these kids. Therefore, Jimmy is rude!
72. Every student brought a pencil or a pen. Marcie brought a pencil. Therefore, Marcie did not bring a pen.
73. If a creature is a chimpanzee, then it is a primate. If a creature is a primate, then it is a mammal. Bobo is a mammal. Therefore, Bobo is a chimpanzee.

For questions [latex]74-76[/latex], name the type of logical fallacy being used.

74. If you don’t want to drive from Boston to New York, then you will have to take the train.
75. New England Patriots quarterback Tom Brady likes his footballs slightly underinflated. The “Cheatriots” have a history of bending or breaking the rules, so Brady must have told the equipment manager to make sure that the footballs were underinflated.
76. Whenever our smoke detector beeps, my kids eat cereal for dinner. The loud beeping sound must make them want to eat cereal for some reason.