The Best Ways to Sample

Identifying the population can be a difficult job, but once we have identified the population, how do we choose an appropriate sample? Remember, although we would prefer to collect data from all members of the population, this is usually impractical unless the population is very small, so we choose a sample.

There are many ways to sample a population, but there is one goal we need to keep in mind: we would like the sample to be representative of the population. One way to ensure that the sample has a reasonable chance of mirroring the population is to employ randomness. The most basic random method is simple random sampling.

Simple Random Sampling

In simple random sampling, every sample of a given size has the same chance of being selected; this results in every individual or entity of the population having an equal chance of being selected.

random sampling

A random sample is one in which each member of the population has an equal probability of being chosen.

 

A simple random sample is one in which every member of the population and any group of members has an equal probability of being chosen.

Recall that random number generators are used to select samples. In the following figure, the random number generator selected numbers [latex]24, 22, 27, 25[/latex], and [latex]13[/latex], resulting in the highlighted individuals being selected for the sample.

Systematic Sampling

In systematic sampling, every individual in the population is given a number and individuals/entities are chosen at regular intervals, with a random starting point (usually among the first several).

systematic sampling

In systematic sampling, every [latex]n[/latex]^th member of the population is selected to be in the sample.

The following figure illustrates a systematic sample where every [latex]4[/latex]th individual is selected, starting at the [latex]3[/latex]rd individual (starting point selected at random). The individuals selected for the sample are highlighted.

Stratified Sampling

In stratified sampling, a population is divided into two or more groups (called strata) according to some criterion (i.e., geographic location, grade level, age group, income group, etc.), and a sample is selected from each strata using simple random sampling or systematic sampling.

stratified sampling

In stratified sampling, a population is divided into a number of subgroups (or strata). Random samples are then taken from each subgroup with sample sizes proportional to the size of the subgroup in the population.

In the illustration below, the population is divided into two groups (blue and green) and [latex]4[/latex] samples were selected from each group.

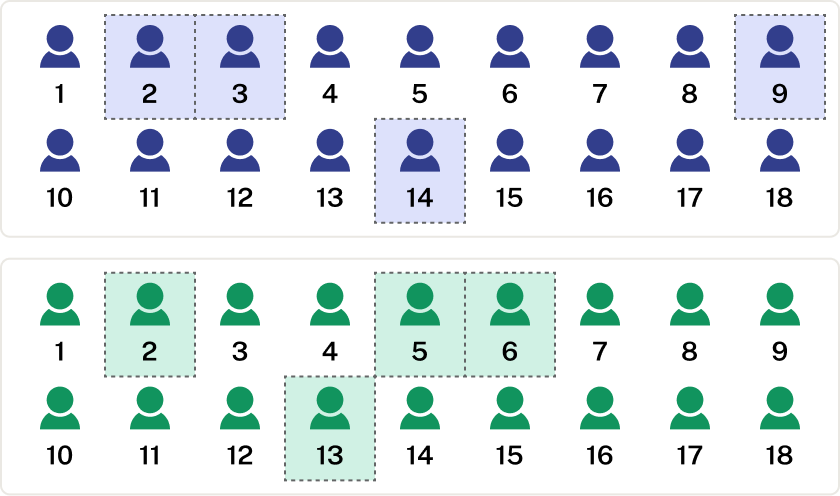
Stratified sampling can also be used to select a sample with people in desired age groups, a specified mix ratio of males and females, etc. A variation on this technique is called quota sampling.

quota sampling

Quota sampling is a variation on stratified sampling, wherein samples are collected in each subgroup until the desired quota is met.

Another sampling method is cluster sampling, in which the population is divided into groups, and one or more groups are randomly selected to be in the sample.

cluster sampling

In cluster sampling, the population is divided into subgroups (clusters), and a set of subgroups are selected to be in the sample.