Sampling and Experimentation: Learn It 1

  • Identify methods for obtaining a random sample of the intended population of a study
  • Identify types of sample bias
  • Identify the differences between observational studies and experiments, and the treatment in an experiment
  • Determine whether an experiment may have been influenced by confounding

Statistical Inference

The process of taking a statistic from a sample and determining a parameter for a population is called statistical inference.

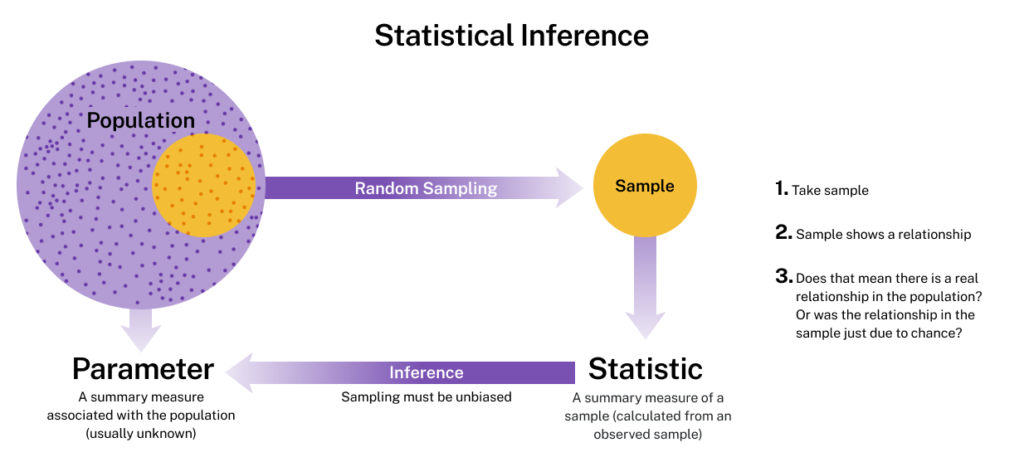
A visual representation of the process of statistical inference. Step 1, take sample. Step 2, sample shows a relationship. Step 3, does that mean there is a real relationship in the population? Or was the relationship in the sample just due to chance? The visual component shows a large purple circle labeled population with a smaller yellow circle in it. There is an arrow labeled random sampling from the large purple circle to a smaller yellow circle labeled Sample. There is an arrow from the sample circle to the word Statistic, which is described as A summary measure of a sample (calculated from an observed sample). There is an arrow from the word statistic labeled Inference and another arrow from the large purple circle to the word Parameter. The arrow labeled inference also says sampling must be unbiased. Underneath the word parameter, it says a summary measure associated with the population (usually unknown)
A population is the group of individuals or entities (such as animals or objects) that our research question pertains to (e.g., all Americans). A sample is a group of individuals or entities on which we collect data. One primary use of statistics is to make inferences about a population based on data collected from a sample from that population. A parameter is a numerical measure that summarizes a population. A statistic is a numerical summary measure of a sample.
Imagine a small college with only [latex]200[/latex] students, and suppose that [latex]60%[/latex] of these students are eligible for financial aid. In this simplified situation, we can identify the population, the variable, and the parameter.

  • Population: [latex]200[/latex] students at the college.
  • Variable: Eligibility for financial aid is a categorical variable, so we use a proportion as a summary.
  • Parameter = Population Proportion: [latex]60%[/latex] students or [latex]0.6[/latex] of the population is eligible for financial aid.

Note: Populations are usually much larger than [latex]200[/latex] people. Also, in real situations, we do not know the population proportion. We are using a simplified situation to investigate how random samples relate to the population. This is the first step in creating a probability model that will be useful in inference. How accurate are random samples at predicting this population proportion of [latex]0.60[/latex]? To answer this question, we randomly select [latex]8[/latex] students and determine the proportion who are eligible for financial aid. We repeat this process several times. Here are the results for [latex]3[/latex] random samples: Financial aid eligibility: 3 random samples of students consisting of 8 students each (out of a total population of 200 students). The proportion eligible for financial aid in the population is .60. In the random samples, each student is assigned a number and then categorized as elibigle for financial aid or not. The sample proportions are as follows: Sample 1 has 6 students eligible for aid and six divided by 8 is 0.75. Sample 2 has 5 students eligible for aid and five divided by 8 is 0.625. Sample 3 has 3 students eligible for aid and three divided by 8 is 0.375. When you average the sample proportions and round to the tens place you get a proportion of .60.

Sampling Bias

Remember that the ideal sample should be representative of the entire population.

In statistics, a sampling bias is created when a sample is collected from a population and some members of the population are not as likely to be chosen as others (remember, each member of the population should have an equally likely chance of being chosen). When a sampling bias happens, there can be incorrect conclusions drawn about the population that is being studied.

sampling bias

Sampling bias occurs when some members of the intended population are less likely to be included in the sample than others, resulting in a sample that is not representative of the population as a whole.

When we say a random sample represents the population well, we mean that there is no inherent bias in this sampling technique. It is important to acknowledge, though, that this does not mean all random samples are necessarily “perfect.”

Random samples are still random, and therefore no random sample will be exactly the same as another. One random sample may give a fairly accurate representation of the population, while another random sample might be “off” purely because of chance. Unfortunately, when looking at a particular sample (which is what happens in practice), we never know how much it differs from the population.