• Organize data using tables, charts, and graphs
• Create and analyze side-by-side and stacked bar graphs
• Create and analyze graphs of quantitative data

Visualizing Data

Categorical, or qualitative, data are pieces of information that allow us to classify the objects under investigation into various categories. We usually begin working with categorical data by summarizing the data into a frequency table.

frequency table

A frequency table is a table with two columns. One column lists the categories, and another for the frequencies with which the items in the categories occur (how many items fit into each category).

An insurance company determines vehicle insurance premiums based on known risk factors. If a person is considered a higher risk, their premiums will be higher. One potential factor is the color of your car. The insurance company believes that people with some color cars are more likely to get in accidents. To research this, they examine police reports for recent total-loss collisions. The data is summarized in the frequency table below.

Color	Frequency
Blue	[latex]25[/latex]
Green	[latex]52[/latex]
Red	[latex]41[/latex]
White	[latex]36[/latex]
Black	[latex]39[/latex]
Grey	[latex]23[/latex]

Sometimes we need an even more intuitive way of displaying data. This is where charts and graphs come in. There are many, many ways of displaying data graphically, but we will concentrate on one very useful type of graph called a bar graph.

bar graph

A bar graph is a graph that displays a bar for each category with the length of each bar indicating the frequency of that category.

 

To construct a bar graph, we need to draw a vertical axis and a horizontal axis. The vertical direction will have a scale and measure the frequency of each category; the horizontal axis has no scale in this instance.

Using our car data from the insurance example at the top of the page, note the highest frequency is [latex]52[/latex], so our vertical axis needs to go from [latex]0[/latex] to [latex]52[/latex], but we might as well use [latex]0[/latex] to [latex]55[/latex], so that we can put a hash mark every [latex]5[/latex] units:

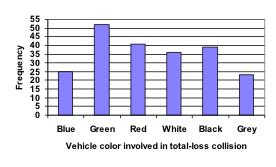
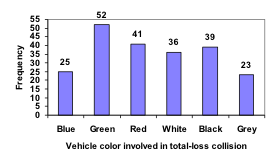
Notice that the height of each bar is determined by the frequency of the corresponding color.  The horizontal gridlines are a nice touch, but not necessary.  In practice, you will find it useful to draw bar graphs using graph paper, so the gridlines will already be in place, or using technology.  Instead of gridlines, we might also list the frequencies at the top of each bar, like this:

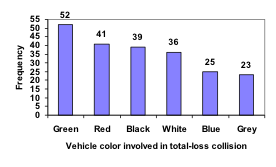
In this case, our chart might benefit from being reordered from largest to smallest frequency values. This arrangement can make it easier to compare similar values in the chart, even without gridlines. When we arrange the categories in decreasing frequency order like this, it is called a Pareto chart.

Pareto chart

A Pareto chart is a bar graph ordered from highest to lowest frequency.

Transforming our bar graph from earlier into a Pareto chart, we get:

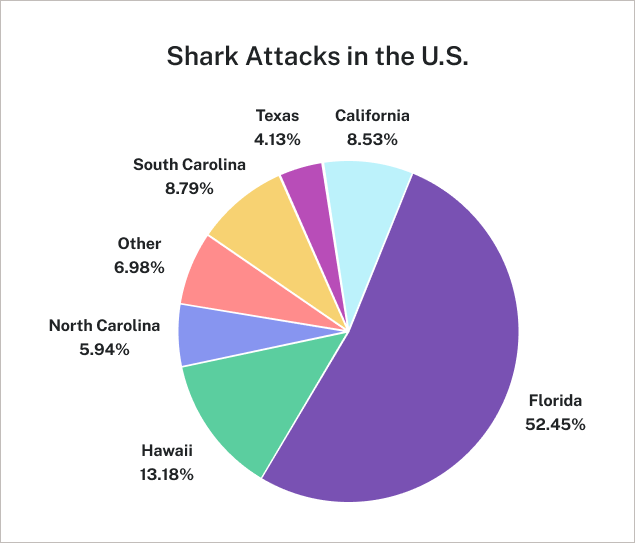
A pie chart is an excellent visual tool for displaying the proportions of each category within a whole, with each ‘slice’ representing the relative size of a part, making it easier to see which categories are larger or smaller at a glance.

pie chart

A pie chart is a circle with wedges cut of varying sizes marked out like slices of pie or pizza.  The relative sizes of the wedges correspond to the relative frequencies of the categories. All pieces of a pie chart should add up to [latex]100\%[/latex].

Create the pie chart for the following data regarding shark attacks in the U.S.

U.S. State	Count	Relative Frequency in Percent (%)
California	[latex]33[/latex]	[latex]8.53[/latex]
Florida	[latex]203[/latex]	[latex]52.45[/latex]
Hawaii	[latex]51[/latex]	[latex]13.18[/latex]
North Carolina	[latex]23[/latex]	[latex]5.94[/latex]
Texas	[latex]16[/latex]	[latex]4.13[/latex]
South Carolina	[latex]34[/latex]	[latex]8.79[/latex]
Other	[latex]27[/latex]	[latex]6.98[/latex]

Show Solution

Pie charts look nice, but are harder to draw by hand than bar charts since to draw them accurately we would need to compute the angle each wedge cuts out of the circle, then measure the angle with a protractor. Computers are much better suited to drawing pie charts. Common software programs like Microsoft Word or Excel, OpenOffice.org, or Google Docs or Sheets are able to create bar graphs, pie charts, and other graph types. There are also numerous online tools that can create graphs.^[1]

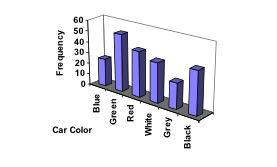
Don’t get fancy with graphs! People sometimes add features to graphs that don’t help to convey their information. For example, [latex]3[/latex]-dimensional bar charts like the one shown below are usually not as effective as their two-dimensional counterparts.

---