Real Numbers: Learn It 1

Lumen Learning

Real Numbers: Learn It 1

Categorize real numbers into counting, whole, rational, irrational, or integers
Recognize and use the properties of real numbers

Defining and Identifying Real Numbers

We have seen that all counting numbers are whole numbers, all whole numbers are integers, and all integers are rational numbers. Irrational numbers are a separate category of their own. When we put together the rational numbers and the irrational numbers, we get the set of real numbers.

real numbers

Real numbers are numbers that are either rational or irrational.

This diagram illustrates the relationships between the different types of real numbers.

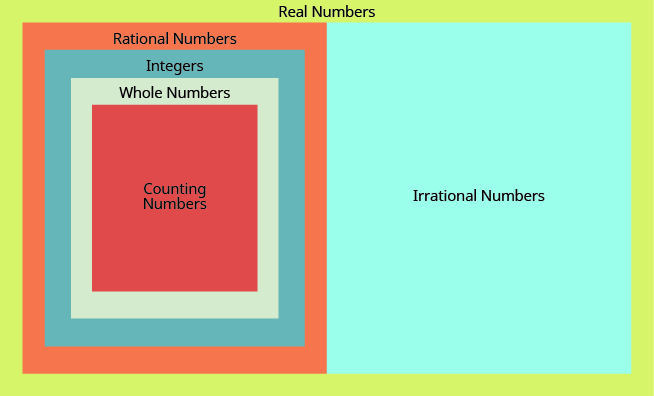
The image shows a large rectangle labeled real numbers. Inside this rectangle, there are two more rectangles labeled rational numbers and irrational numbers. Inside the rational numbers rectangle, there is a rectangle labeled integers. Inside of that rectangle, there is another rectangle labeled whole numbers. Inside of that rectangle is a square labeled counting numbers.

Natural Numbers or Counting Numbers: Start with [latex]1[/latex] and continue. [latex]1,2,3,4,5…[/latex]
Whole Numbers: Counting numbers plus zero. [latex]0,1,2,3,4,5…[/latex]
Integers: Whole numbers and their negative counterparts.
Rational Numbers: Numbers that can be written in the form [latex]{\Large\frac{a}{b}}[/latex], where [latex]a[/latex] and [latex]b[/latex] are integers and [latex]b\ne o[/latex]. In decimal form, the numbers terminate or repeat.
Irrational Numbers: Numbers that can’t be expressed as a simple fraction. In decimal form, the numbers do not repeat or terminate.

Does the term “real numbers” seem strange to you? Are there any numbers that are not “real”, and, if so, what could they be?

For centuries, the only numbers people knew about were what we now call the real numbers. Then mathematicians discovered the set of imaginary numbers.

An imaginary number is a number that, when squared, has a negative result, typically expressed as a real number multiplied by the imaginary unit [latex]i[/latex], where [latex]i^2=−1[/latex]. We won’t discuss imaginary numbers in this section, but you may encounter them in other places in this course.

Determine whether each of the numbers in the following list is a

whole number
integer
rational number
irrational number
real number

[latex]-7[/latex], [latex]\frac{14}{5}[/latex], [latex]8[/latex], [latex]\sqrt{5}[/latex], [latex]5.9[/latex], [latex]-\sqrt{64}[/latex]

Number	[latex]-7[/latex]	[latex]\frac{14}{5}[/latex]	[latex]8[/latex]	[latex]\sqrt{5}[/latex]	[latex]5.9[/latex]	[latex]-\sqrt{64}[/latex]
Whole			[latex]\quad\checkmark[/latex]
Integer	[latex]\quad\checkmark[/latex]		[latex]\quad\checkmark[/latex]			[latex]\quad\checkmark[/latex]
Rational	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]		[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]
Irrational				[latex]\quad\checkmark[/latex]
Real	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]	[latex]\quad\checkmark[/latex]