Name Decimals
In the following exercises, name each decimal.
- five and five tenths
- five and one hundredth
- eight and seventy-one hundredths
- two thousandths
- three hundred eighty-one thousandths
- negative seventeen and nine tenths
Write Decimals
In the following exercises, translate the name into a decimal number.
- [latex]8.03[/latex]
- [latex]29.81[/latex]
- [latex]0.7[/latex]
- [latex]0.001[/latex]
- [latex]0.029[/latex]
- [latex]−11.0009[/latex]
- [latex]13.0395[/latex]
Convert Decimals to Fractions or Mixed Numbers
In the following exercises, convert each decimal to a fraction or mixed number.
- [latex]1 \frac{99}{100}[/latex]
- [latex]15 \frac{7}{10}[/latex]
- [latex]\frac{239}{1000}[/latex]
- [latex]\frac{13}{100}[/latex]
- [latex]\frac{11}{1000}[/latex]
- [latex]- \frac{7}{100000}[/latex]
- [latex]6 \frac{2}{5}[/latex]
- [latex]7 \frac{1}{20}[/latex]
- [latex]4 \frac{3}{500}[/latex]
- [latex]10 \frac{1}{4}[/latex]
- [latex]1 \frac{81}{250}[/latex]
- [latex]14 \frac{1}{8}[/latex]
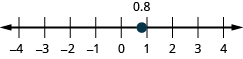
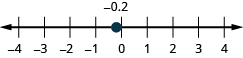
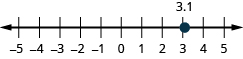
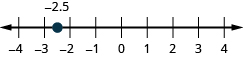
Locate Decimals on the Number Line
Order Decimals
In the following exercises, order each of the following pairs of numbers, using [latex]< or >[/latex].
- [latex]>[/latex]
- [latex]<[/latex]
- [latex]>[/latex]
- [latex]>[/latex]
- [latex]<[/latex]
- [latex]<[/latex]
Round Decimals
In the following exercises, round each number to the nearest tenth.
- [latex]0.7[/latex]
- [latex]2.8[/latex]
In the following exercises, round each number to the nearest hundredth.
- [latex]0.85[/latex]
- [latex]5.79[/latex]
- [latex]0.30[/latex]
- [latex]4.10[/latex]
In the following exercises, round each number to the nearest ⓐ hundredth ⓑ tenth ⓒ whole number.
- ⓐ [latex]5.78[/latex] ⓑ [latex]5.8[/latex] ⓒ [latex]6[/latex]
- ⓐ [latex]63.48[/latex] ⓑ [latex]63.5[/latex] ⓒ [latex]63[/latex]
Operations on Decimals
Add and Subtract Decimals
In the following exercises, add or subtract.
- [latex]24.48[/latex]
- [latex]170.88[/latex]
- [latex]−9.23[/latex]
- [latex]49.73[/latex]
- [latex]−40.91[/latex]
- [latex]−7.22[/latex]
- [latex]−13.5[/latex]
- [latex]35.8[/latex]
- [latex]−27.5[/latex]
- [latex]15.73[/latex]
- [latex]42.51[/latex]
- [latex]102.212[/latex]
- [latex]51.31[/latex]
- [latex]−4.89[/latex]
Multiply Decimals
In the following exercises, multiply.
- [latex]0.12[/latex]
- [latex]0.144[/latex]
- [latex]42.008[/latex]
- [latex]26.7528[/latex]
- [latex]−11.653[/latex]
- [latex]337.8914[/latex]
- [latex]2.2302[/latex]
- [latex]1.305[/latex]
- [latex]92.4[/latex]
- [latex]55,200[/latex]
Divide Decimals
In the following exercises, divide.
- [latex]0.03[/latex]
- [latex]0.19[/latex]
- [latex]$0.71[/latex]
- [latex]$2.44[/latex]
- [latex]3[/latex]
- [latex]−4.8[/latex]
- [latex]35[/latex]
- [latex]2.08[/latex]
- [latex]150[/latex]
- [latex]20[/latex]
Mixed Practice
In the following exercises, simplify.
- [latex]19.2[/latex]
- [latex]12.09[/latex]
- [latex]32.706[/latex]
- [latex]$48.60[/latex]
- [latex]20[/latex]
- [latex]2[/latex]
- [latex]$17.80[/latex]
Use Decimals in Money Applications
In the following exercises, use the strategy for applications to solve.
- [latex]$24.89[/latex]
- [latex]$29.06[/latex]
- [latex]$3.19[/latex]
- [latex]181.7 pounds[/latex]
- [latex]$15.00[/latex]
- [latex]$296.00[/latex]
- [latex]$12.75[/latex]
-
- [latex]$3[/latex]
- [latex]$1.50[/latex]
- [latex]$1[/latex]
- [latex]$18.64[/latex]
- [latex]$259.45[/latex]
Exploring The Relationship Between Decimals and Fractions
Convert Fractions to Decimals
- [latex]0.4[/latex]
- [latex]−0.375[/latex]
- [latex]0.85[/latex]
- [latex]2.75[/latex]
- [latex]−12.4[/latex]
- [latex]-0.5[/latex]
- [latex]-1.36[/latex]
- [latex]-0.135[/latex]
Convert Fractions to Decimals and Simplify
In the following exercises, simplify the expression.
- [latex]7[/latex]
- [latex]3.025[/latex]
- [latex]10.58[/latex]
Order Decimals and Fractions
In the following exercises, order each pair of numbers, using [latex]< or >[/latex].
- [latex]<[/latex]
- [latex]>[/latex]
- [latex]<[/latex]
- [latex]<[/latex]
- [latex]>[/latex]
- [latex]>[/latex]
- [latex]0.55, \frac{9}{16}, \frac{3}{5}[/latex]
- [latex]\frac{5}{8}, \frac{13}{20}, 0.702[/latex]
- [latex]- \frac{7}{20}, - \frac{1}{3}, -0.3[/latex]
- [latex]- \frac{7}{9}, - \frac{3}{4}, -0.7[/latex]
- [latex]−187[/latex]
- [latex]295.12[/latex]
- [latex]6.15[/latex]
- [latex]20.2[/latex]
- [latex]107.11[/latex]
- [latex]449[/latex]
- [latex]9.14[/latex]
- [latex]−0.23[/latex]
- [latex]−3.25[/latex]
- [latex]16.29[/latex]
- [latex]632.045[/latex]
- [latex]−5.742[/latex]
Find the Circumference and Area of Circles
- [latex]31.4[/latex] in ⓑ [latex]78.5[/latex] sq. in
- [latex]56.52[/latex] ft ⓑ [latex]254.34[/latex] sq. ft
- [latex]288.88[/latex] cm ⓑ [latex]6644.24[/latex] sq. cm
- [latex]116.808/latex] m ⓑ [latex]1086.3144/latex] sq. ml
- ⓐ [latex]\frac{22}{5}[/latex] mile ⓑ [latex]frac{77}{50}[/latex] sq. mile
- ⓐ [latex]\frac{33}{14}[/latex] yard ⓑ[latex]\frac{99}{224}[/latex] sq. yard
- ⓐ no ⓑ no ⓒ yes
- ⓐ no ⓑ yes ⓒ no
- [latex]y = 2.8[/latex]
- [latex]f = −0.85[/latex]
- [latex]a = −7.9[/latex]
- [latex]c = −4.65[/latex]
- [latex]n = 4.4[/latex]
- [latex]x = −3.5[/latex]
- [latex]j = −4.68[/latex]
- [latex]m = −1.42[/latex]
- [latex]x = 7[/latex]
- [latex]c = −5[/latex]
- [latex]p = 3[/latex]
- [latex]q = −80[/latex]
- [latex]x = 20[/latex]
- [latex]z = 2.7[/latex]
- [latex]a = −8[/latex]
- [latex]x = −0.28[/latex]
- [latex]p = 8.25[/latex]
- [latex]r = 7.2[/latex]
Mixed Practice
- [latex]x = −6[/latex]
- [latex]p = −10[/latex]
- [latex]m = 8[/latex]
- [latex]q = - \frac{3}{4}[/latex]
- [latex]n-1.9 = 3.4; 5.3[/latex]
- [latex]−6.2x = −4.96; 0.8[/latex]
- [latex]\frac{y}{-1.7} = -5; 8.5[/latex]
- [latex]n + (−7.3) = 2.4; 9.7[/latex]
Name Decimals
- three hundred seventy-five thousandths
- five and twenty-four hundredths
- negative four and nine hundredths
- [latex]0.09[/latex]
- [latex]10.035[/latex]
- [latex]−0.05[/latex]
- [latex]\frac{33}{40}[/latex]
- [latex]3 \frac{16}{25}[/latex]
- [latex]<[/latex]
- [latex]<[/latex]
- ⓐ [latex]12.53[/latex] ⓑ [latex]12.5[/latex] ⓒ [latex]13[/latex]
- ⓐ [latex]5.90[/latex] ⓑ [latex]5.9[/latex] ⓒ [latex]6[/latex]
- [latex]24.67[/latex]
- [latex]24.831[/latex]
- [latex]−2.37[/latex]
Multiply Decimals
- [latex]−1.6[/latex]
- [latex]15,400[/latex]
- [latex]0.18[/latex]
- [latex]4[/latex]
- [latex]200[/latex]
- [latex]$28.22[/latex]
- [latex]$1.79[/latex]
- [latex]0.875[/latex]
- [latex]−5.25[/latex]
- [latex]−0.54[/latex]
Order Decimals and Fractions
In the following exercises, order each pair of numbers, using [latex]< or >[/latex]
- [latex]>[/latex]
- [latex]>[/latex]
- [latex]>[/latex]
- [latex]\frac{11}{15}, 0.75, \frac{7}{9}[/latex]
- [latex]6.03[/latex]
- [latex]1.975[/latex]
- [latex]−0.22[/latex]
- ⓐ [latex]21.98[/latex] ft. ⓑ [latex]38.465[/latex] sq. ft.
- ⓐ [latex]34.54[/latex] cm ⓑ [latex]379.94[/latex] sq. cm
Use the Definition of Percents
- [latex]\frac{6}{100}[/latex]
- [latex]\frac{32}{1000}[/latex]
- ⓐ [latex]\frac{57}{100}[/latex] ⓑ [latex]57\%[/latex]
- ⓐ [latex]\frac{42}{100}[/latex] ⓑ [latex]42\%[/latex]
- [latex]\frac{1}{25}[/latex]
- [latex]\frac{17}{100}[/latex]
- [latex]\frac{13}{25}[/latex]
- [latex]\frac{5}{4}[/latex]
- [latex]\frac{3}{8}[/latex]
- [latex]\frac{23}{125}[/latex]
- [latex]0.05[/latex]
- [latex]0.01[/latex]
- [latex]0.63[/latex]
- [latex]0.4[/latex]
- [latex]1.15[/latex]
- [latex]1.5[/latex]
- [latex]0.214[/latex]
- [latex]0.078[/latex]
- ⓐ [latex]\frac{3}{200}[/latex] ⓑ [latex]0.015[/latex]
- ⓐ [latex]\frac{7023}{10000}[/latex] ⓑ [latex]0.7023[/latex]
- ⓐ [latex]\frac{1}{4}[/latex] ⓑ[latex]0.25[/latex]
- ⓐ [latex]\frac{3}{5}[/latex] ⓑ[latex]0.6[/latex]
- [latex]1\%[/latex]
- [latex]18\%[/latex]
- [latex]135\%[/latex]
- [latex]300\%[/latex]
- [latex]0.9\%[/latex]
- [latex]8.75\%[/latex]
- [latex]150\%[/latex]
- [latex]225.4\%[/latex]
- [latex]25\%[/latex]
- [latex]37.5\%[/latex]
- [latex]175\%[/latex]
- [latex]680\%[/latex]
- [latex]41.7\%[/latex]
- [latex]266.6\%[/latex]
- [latex]42.9\%[/latex]
- [latex]55.6\%[/latex]
- [latex]25\%[/latex]
- [latex]35\%[/latex]
Translate and Solve Basic Percent Equations
- [latex]54[/latex]
- [latex]26.88[/latex]
- [latex]162.5[/latex]
- [latex]18,000[/latex]
- [latex]112[/latex]
- [latex]108[/latex]
- [latex]$35[/latex]
- [latex]$940[/latex]
- [latex]30\%[/latex]
- [latex]36\%[/latex]
- [latex]150%[/latex]
- [latex]175%[/latex]
Solve Applications of Percents
- [latex]$11.88[/latex]
- [latex]$259.80[/latex]
- [latex]24.2[/latex] grams
- [latex]2,407[/latex] grams
- [latex]45\%[/latex]
- [latex]25\%[/latex]
Find Percent Increase and Percent Decrease
- [latex]13.2\%[/latex]
- [latex]125\%[/latex]
- [latex]72.7\%[/latex]
- [latex]2.5\%[/latex]
- [latex]11\%[/latex]
- [latex]5.5\%[/latex]
- ⓐ [latex]$4.20[/latex] ⓑ [latex]$88.20[/latex]
- ⓐ [latex]$9.68[/latex] ⓑ [latex]$138.68[/latex]
- ⓐ [latex]$17.13[/latex] ⓑ [latex]$267.13[/latex]
- ⓐ [latex]$61.45[/latex] ⓑ [latex]$1,260.45[/latex]
- [latex]6.5\%[/latex]
- [latex]6.85\%[/latex]
- [latex]$20.25[/latex]
- [latex]$975[/latex]
- [latex]$859.25[/latex]
- [latex]3\%[/latex]
- [latex]16\%[/latex]
- [latex]15.5\%[/latex]
- [latex]$139[/latex]
- [latex]$125[/latex]
- ⓐ [latex]$26.97[/latex] ⓑ [latex]$17.98[/latex]
- ⓐ [latex]$128.37[/latex] ⓑ [latex]$260.63[/latex]
- ⓐ [latex]$332.48[/latex] ⓑ [latex]$617.50[/latex]
- ⓐ[latex]$576[/latex] ⓑ [latex]30\%[/latex]
- ⓐ [latex]$53.25[/latex] ⓑ [latex]15\%[/latex]
- ⓐ [latex]$370[/latex] ⓑ [latex]43.5\%[/latex]
Solve Mark-up Applications
- ⓐ [latex]$7.20[/latex] ⓑ [latex]$23.20[/latex]
- ⓐ $[latex]0.20[/latex] ⓑ [latex]$0.80[/latex]
- ⓐ [latex]$258.75[/latex] ⓑ [latex]$373.75[/latex]
- [latex]$90[/latex]
- [latex]$579.96[/latex]
- [latex]$14,167[/latex]
- [latex]$3,280[/latex]
- [latex]$860[/latex]
- [latex]$24,679.91[/latex]
- [latex]4\%[/latex]
- [latex]5.5\%[/latex]
- [latex]$116[/latex]
- [latex]$4,836[/latex]
- [latex]3\%[/latex]
- [latex]3.75\%[/latex]
- [latex]$35,000[/latex]
- [latex]$3,345[/latex]
- [latex]$332.10[/latex]
- [latex]$195.00[/latex]
Solving Proportions and their Applications
- [latex]\frac{4}{15} = \frac{36}{135}[/latex]
- [latex]\frac{12}{5} = \frac{96}{40}[/latex]
- [latex]\frac{5}{7} = \frac{115}{161}[/latex]
- [latex]\frac{8}{1} = \frac{48}{6}[/latex]
- [latex]\frac{9.36}{18} = \frac{2.6}{5}[/latex]
- [latex]\frac{18.04}{11} = \frac{4.92}{3}[/latex]
- yes
- no
- no
- yes
- [latex]x = 49[/latex]
- [latex]z = 7[/latex]
- [latex]a = 9[/latex]
- [latex]p = -11[/latex]
- [latex]a = 7[/latex]
- [latex]c = 2[/latex]
- [latex]j = 0.6[/latex]
- [latex]m = 4[/latex]
- [latex]9[/latex] ml
- [latex]114[/latex], no
- [latex]159[/latex] cal
- [latex]\frac{3}{4}[/latex] cup
- [latex]$252.50[/latex]
- [latex]1.25[/latex]
- [latex]48[/latex] quarters
- [latex]19, $58.71[/latex]
- [latex]12.8[/latex] hours
- [latex]4[/latex] bags
- [latex]\frac{n}{250} = \frac{35}{100}[/latex]
- [latex]\frac{n}{47} = \frac{110}{100}[/latex]
- [latex]\frac{45}{n} = \frac{30}{100}[/latex]
- [latex]\frac{90}{n} = \frac{150}{100}[/latex]
- [latex]\frac{17}{85} = \frac{p}{100}[/latex]
- [latex]\frac{340}{260} = \frac{p}{100}[/latex]
- [latex]117[/latex]
- [latex]16.56[/latex]
- [latex]45.5[/latex]
- [latex]1464[/latex]
- [latex]$45[/latex]
- [latex]$164[/latex]
- [latex]25\%[/latex]
- [latex]12.5\%[/latex]
Using the Language of Algebra
Use Variables and Algebraic Symbols
- [latex]16[/latex] minus [latex]9[/latex], the difference of sixteen and nine
- [latex]5[/latex] times [latex]6[/latex], the product of five and six
- [latex]28[/latex] divided by [latex]4[/latex], the quotient of twenty-eight and four
- [latex]x[/latex] plus [latex]8[/latex], the sum of [latex]x[/latex] and eight
- [latex]2[/latex] times [latex]7[/latex], the product of two and seven
- fourteen is less than twenty-one
- thirty-six is greater than or equal to nineteen
- [latex]3[/latex] times [latex]n[/latex] equals [latex]24[/latex], the product of three and [latex]n[/latex] equals twenty-four
- [latex]y[/latex] minus [latex]1[/latex] is greater than [latex]6[/latex], the difference of [latex]y[/latex] and one is greater than six
- [latex]2[/latex] is less than or equal to [latex]18[/latex] divided by [latex]6[/latex]; [latex]2[/latex] is less than or equal to the quotient of eighteen and six
- [latex]2[/latex] is less than or equal to [latex]18[/latex] divided by [latex]6[/latex]; [latex]2[/latex] is less than or equal to the quotient of eighteen and six
Identify Expressions and Equations
In the following exercises, determine if each is an expression or an equation.
- equation
- expression
- expression
- equation
Simplify Expressions with Exponents
In the following exercises, write in exponential form.
- [latex]3^{7}[/latex]
- [latex]x^{5}[/latex]
Simplify Expressions with Exponents
In the following exercises, write in expanded form.
- [latex]125[/latex]
- [latex]256[/latex]
Simplify Expressions Using the Order of Operations
In the following exercises, simplify.
- [latex]43[/latex]
- [latex]55[/latex]
- [latex]5[/latex]
- [latex]34[/latex]
- [latex]58[/latex]
- [latex]6[/latex]
- [latex]13[/latex]
- [latex]4[/latex]
- [latex]35[/latex]
- [latex]10[/latex]
- [latex]41[/latex]
- [latex]81[/latex]
- [latex]149[/latex]
- [latex]50[/latex]
Evaluating, Simplifying, and Translating Algebraic Expressions
Evaluate Algebraic Expressions
In the following exercises, evaluate the expression for the given value.
- [latex]22[/latex]
- [latex]26[/latex]
- [latex]144[/latex]
- [latex]32[/latex]
- [latex]27[/latex]
- [latex]21[/latex]
- [latex]41[/latex]
- [latex]9[/latex]
- [latex]73[/latex]
- [latex]73[/latex]
- [latex]54[/latex]
Identify Terms, Coefficients, and Like Terms
In the following exercises, list the terms in the given expression.
- [latex]15x^{2}, 6x, 2[/latex]
- [latex]10y^{3}, y, 2[/latex]
- [latex]8[/latex]
- [latex]5[/latex]
- [latex]x^{3}[/latex], [latex]8x^{3}[/latex] and [latex]14, 5[/latex]
- [latex]16ab[/latex] and [latex]4ab[/latex]; [latex]16b^{2}[/latex] and [latex]9b^{2}[/latex]
Simplify Expressions by Combining Like Terms
In the following exercises, simplify the given expression by combining like terms.
- [latex]13x[/latex]
- [latex]26a[/latex]
- [latex]7c[/latex]
- [latex]12x + 8[/latex]
- [latex]10u + 3[/latex]
- [latex]12p + 10[/latex]
- [latex]22a + 1[/latex]
- [latex]17x^{2} + 20x + 16[/latex]
Translate English Phrases into Algebraic Expressions
In the following exercises, translate the given word phrase into an algebraic expression.
- [latex]8 + 12[/latex]
- [latex]14 − 9[/latex]
- [latex]9 ⋅ 7[/latex]
- [latex]36 ÷ 9[/latex]
- [latex]x − 4[/latex]
- [latex]6y[/latex]
- [latex]8x + 3x[/latex]
- [latex]\frac{y}{3}[/latex]
- [latex]8 (y − 9)[/latex]
- [latex]5 (x + y)[/latex]
Translate English Phrases into Algebraic Expressions
In the following exercises, write an algebraic expression.
- [latex]b + 15[/latex]
- [latex]b − 4[/latex]
- [latex]2n − 7[/latex]