Recognizing Interpolation or Extrapolation

Understanding the difference between correlation and causation is crucial for interpreting data accurately. Similarly, knowing when to use interpolation and extrapolation is vital for making meaningful predictions or estimations based on existing data. Both skills are key to being a savvy consumer and interpreter of data.

We use a process known as interpolation when we predict a value inside the domain and range of the data. The process of extrapolation is used when we predict a value outside the domain and range of the data.

interpolation and extrapolation

Different methods of making predictions are used to analyze data.

 

The method of interpolation involves predicting a value inside the domain and/or range of the data.

The method of extrapolation involves predicting a value outside the domain and/or range of the data.

The table below shows the number of cricket chirps in [latex]15[/latex] seconds, for several different air temperatures, in degrees Fahrenheit¹.

Chirps	[latex]44[/latex]	[latex]35[/latex]	[latex]20.4[/latex]	[latex]33[/latex]	[latex]31[/latex]	[latex]35[/latex]	[latex]18.5[/latex]	[latex]37[/latex]	[latex]26[/latex]
Temperature	[latex]80.5[/latex]	[latex]70.5[/latex]	[latex]57[/latex]	[latex]66[/latex]	[latex]68[/latex]	[latex]72[/latex]	[latex]52[/latex]	[latex]73.5[/latex]	[latex]53[/latex]

 

We can plot these data points and compare the process of interpolation and extrapolation of the data.

 

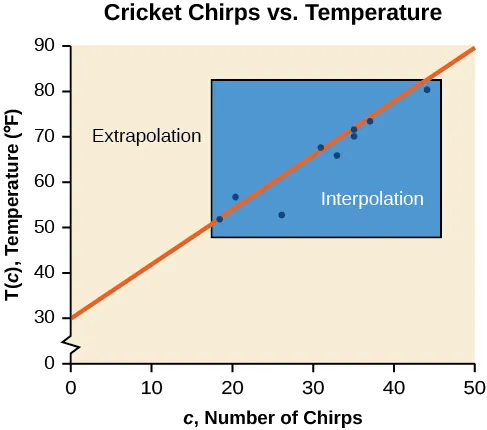
We can see that interpolation would occur if we used our model to predict temperature when the values for chirps are between [latex]18.5[/latex] and [latex]44[/latex]. Extrapolation would occur if we used our model to predict temperature when the values for chirps are less than [latex]18.5[/latex] or greater than [latex]44[/latex].

There is a difference between making predictions inside the domain and range of values for which we have data and outside that domain and range. Predicting a value outside of the domain and range has its limitations. When our model no longer applies after a certain point, it is sometimes called model breakdown.

model breakdown

Model breakdown occurs at the point when the model no longer applies.

Predicting a cost function for a period of two years may involve examining the data where the input is the time in years and the output is the cost. But if we try to extrapolate a cost when [latex]x=50[/latex], that is in [latex]50[/latex] years, the model would not apply because we could not account for factors fifty years in the future.

When to Use Interpolation and Extrapolation

Interpolation is your go-to method when you have a set of data points and you’re interested in estimating a value that falls within the known range of these points. It’s particularly useful in scenarios where the data follows a consistent pattern or trend.

On the other hand, extrapolation is more suitable for making predictions that extend beyond your existing data set. However, it’s important to note that extrapolation comes with a higher degree of uncertainty and should be used cautiously, especially when the data set is small or the variables involved are subject to rapid change.

Use the information given in the previous example showing the number of cricket chirps in [latex]15[/latex] seconds and the model [latex]T(c) = 1.2c+30[/latex] to answer the following questions:

1. Would predicting the temperature when crickets are chirping [latex]30[/latex] times in [latex]15[/latex] seconds be interpolation or extrapolation? Make the prediction, and discuss whether it is reasonable.
2. Would predicting the number of chirps crickets will make at [latex]40[/latex] degrees be interpolation or extrapolation? Make the prediction, and discuss whether it is reasonable.

Show Answer

1. The number of chirps in the data provided varied from [latex]18.5[/latex] to [latex]44[/latex]. A prediction at [latex]30[/latex] chirps per [latex]15[/latex] seconds is inside the domain of our data, so would be interpolation. Using our model:

   [latex]\begin{array}{lll} T(30) & = 30 + 1.2(30) & \text{(Given)} \\ & = 30 + 36 & \text{(Simplify the multiplication)} \\ & = 66 \text{ degrees} & \text{(Add the numbers)} \\ \end{array}[/latex]

   Based on the data we have, this value seems reasonable.

2. The temperature values varied from [latex]52[/latex] to [latex]80.5[/latex]. Predicting the number of chirps at [latex]40[/latex] degrees is extrapolation because [latex]40[/latex] is outside the range of our data. Using our model:

   [latex]\begin{array}{lll} 40 & = 30 + 1.2c & \text{(Given)} \\ 10 & = 1.2c & \text{(Subtract 30 from both sides)} \\ c & \approx 8.33 & \text{(Divide both sides by 1.2)} \\ \end{array}[/latex]

We can compare the regions of interpolation and extrapolation using the figure given before.

 

Analysis Our model predicts the crickets would chirp [latex]8.33[/latex] times in [latex]15[/latex] seconds. While this might be possible, we have no reason to believe our model is valid outside the domain and range. In fact, generally crickets stop chirping altogether below around [latex]50[/latex] degrees.

Risks and Limitations

Interpolation carries the inherent risk of assuming that the data between known points will follow the same pattern as the data points you have. This can be a reasonable assumption in many scientific and engineering contexts, but it’s not always valid. For example, if you’re interpolating temperature data, a sudden weather event that wasn’t accounted for could make your estimates inaccurate.

Extrapolation poses even greater risks because it assumes that a current trend will continue indefinitely into the future. This is a bold assumption and often not true in real-world scenarios. For instance, if you’re extrapolating sales data for a product, market saturation or the entry of a competitor could drastically alter future sales, making your extrapolation misleading.