Math in Arts: Background You’ll Need 2

  • Identify how functions flip

Vertical Reflection

Another transformation that can be applied to a function is a reflection over the [latex]x[/latex]– or [latex]y[/latex]-axis. A vertical reflection reflects a graph vertically across the [latex]x[/latex]-axis, while a horizontal reflection reflects a graph horizontally across the [latex]y[/latex]-axis. The reflections are shown in the figure below.

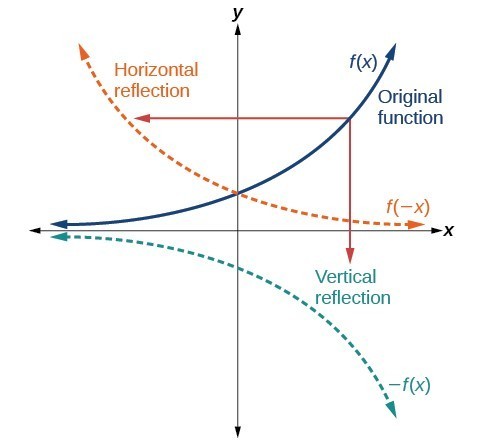
Graph of the vertical and horizontal reflection of a function.
Vertical and horizontal reflections of a function.

 

Notice that the vertical reflection produces a new graph that is a mirror image of the base or original graph about the [latex]x[/latex]-axis. The horizontal reflection produces a new graph that is a mirror image of the base or original graph about the [latex]y[/latex]-axis.

vertical reflection

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=-f\left(x\right)[/latex] is a vertical reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about (or over, or through) the [latex]x[/latex]-axis.

horizontal reflection

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(-x\right)[/latex] is a horizontal reflection of the function [latex]f\left(x\right)[/latex], sometimes called a reflection about the [latex]y[/latex]-axis.