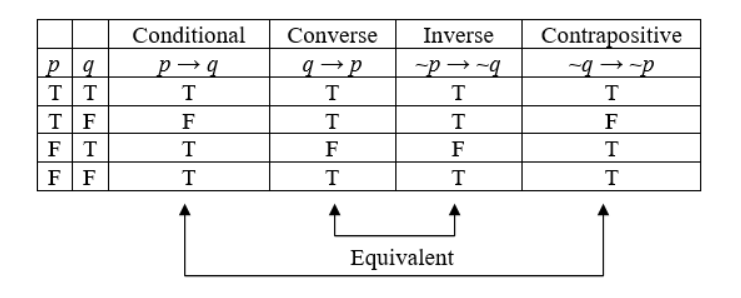
Equivalence
Looking at truth tables, we can see that the original conditional and the contrapositive are logically equivalent, and that the converse and inverse are logically equivalent.
equivalence
Statements [latex]p[/latex] and [latex]q[/latex] are said to be logically equivalent if they have the same truth value in every model.
- A conditional statement and its contrapositive are logically equivalent.
- The converse and inverse of a statement are logically equivalent.
In other words, the original statement and the contrapositive must agree with each other; they must both be true, or they must both be false. Similarly, the converse and the inverse must agree with each other; they must both be true, or they must both be false.
DeMorgan’s Laws
There are two pairs of logically equivalent statements that come up again and again in logic. They are prevalent enough to be dignified by a special name: DeMorgan’s laws.
Before we can dive into these laws, it is important to understand the term “negation.” Given a statement [latex]R[/latex], the statement [latex]\sim{R}[/latex] is called the negation of [latex]R[/latex]. If [latex]R[/latex] is a complex statement, then it is often the case that its negation [latex]\sim{R}[/latex] can be written in a simpler or more useful form. The process of finding this form is called negating [latex]R[/latex]. In proving theorems it is often necessary to negate certain statements.
DeMorgan’s laws
- The negation of a conjunction is equivalent to the disjunction of the negation of the statements making up the conjunction. To negate an “and” statement, negate each part and change the “and” to “or”.
[latex]\sim\left(P{\wedge}Q\right)=({\sim}P)\vee\left(\sim{Q}\right)[/latex]
- The negation of a disjunction is equivalent to the conjunction of the negation of the statements making up the disjunction. To negate an “or” statement, negate each part and change the “or” to “and”.
[latex]\sim\left(P\vee{Q}\right)=\left(\sim{P}\right)\wedge\left(\sim{Q}\right)[/latex]
Still, De Morgan is given credit for stating the laws in the terms of modern formal logic, and incorporating them into the language of logic. De Morgan’s laws can be proved easily, and may even seem trivial. Nonetheless, these laws are helpful in making valid inferences in proofs and deductive arguments.
DeMorgan’s laws are actually very natural and intuitive. Consider the statement [latex]\sim\left(P\wedge{Q}\right)[/latex], which we can interpret as meaning that it is not the case that both [latex]P[/latex] and [latex]Q[/latex] are true. If it is not the case that both [latex]P[/latex] and [latex]Q[/latex] are true, then at least one of [latex]P[/latex] or [latex]Q[/latex] is false, in which case [latex]\left(\sim{P}\right)\vee\left(\sim{Q}\right)[/latex] is true. Thus [latex]\sim\left(P\wedge{Q}\right)[/latex] means the same thing as [latex]\left(\sim{P}\right)\vee\left(\sim{Q}\right)[/latex]. This law can also be verified using a truth table.
| [latex]P[/latex] | [latex]Q[/latex] | [latex]\sim{P}[/latex] | [latex]\sim{Q}[/latex] | [latex]P\wedge{Q}[/latex] | [latex]\sim\left(P\wedge{Q}\right)[/latex] | [latex]\left(\sim{P}\right)\vee\left(\sim{Q}\right)[/latex] |
|---|---|---|---|---|---|---|
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | T |
| F | T | T | F | F | T | T |
| F | F | T | T | F | T | T |
DeMorgan’s laws can be very useful. Suppose we happen to know that some statement having form [latex]\sim\left(P\vee{Q}\right)[/latex] is true. The second of DeMorgan’s laws tells us that [latex]\left(\sim{Q}\right)\wedge\left(\sim{P}\right)[/latex] is also true, hence [latex]\sim{P}[/latex] and [latex]\sim{Q}[/latex] are both true as well. Being able to quickly obtain such additional pieces of information can be extremely useful.
Here is a summary of some significant logical equivalences. Those that are not immediately obvious can be verified with a truth table.
\text{Contrapositive law} & P\rightarrow{Q}=(\sim{Q})\rightarrow(\sim{P}) \\[6pt]
\text{DeMorgan's laws} & \sim(P\land{Q})=\sim{P}\lor\sim{Q} \\
& \sim(P\lor{Q})=\sim{P}\land\sim{Q} \\[6pt]
\text{Commutative laws} & (P\land{Q})={P}\land{Q} \\
& (P\lor{Q})={P}\lor{Q} \\[6pt]
\text{Distributive laws} & {P}\land(Q\lor{R})=({P}\land{Q})\lor(P\land{R}) \\
& P\lor(Q\land{R})=({P}\lor{Q})\land(P\lor{R}) \\[6pt]
\text{Associative laws} & P\land(Q\land{R})=(P\land{Q})\land{R} \\
& P\lor(Q\lor{R})=(P\lor{Q})\lor{R} \\
\end{array}[/latex]
Notice how the distributive law [latex]P\wedge\left(Q\vee{R}\right)=\left(P\wedge{Q}\right)\vee\left(P\wedge{Q}\right)\vee\left(P\wedge{R}\right)[/latex] has the same structure as the distributive law [latex]p\left(q+r\right)=p\cdot{q}+p\cdot{r}[/latex] from algebra. Concerning the associative laws, the fact that [latex]P\wedge\left(Q\wedge{R}\right)=\left(P\wedge{Q}\right)\wedge{R}[/latex] means that the position of the parentheses is irrelevant, and we can write this as [latex]P\wedge{Q}\wedge{R}[/latex] without ambiguity. Similarly, we may drop the parentheses in an expression such as [latex]P\vee\left(Q\vee{R}\right)[/latex].
But parentheses are essential when there is a mix of [latex]\wedge[/latex] and [latex]\vee[/latex], as in [latex]P\vee\left(Q\wedge{R}\right)[/latex]. Indeed, [latex]P\vee\left(Q\wedge{R}\right)[/latex] and [latex]P\vee\left(Q\wedge{R}\right)[/latex] and [latex]P\vee\left({Q}\right)\wedge{R}[/latex] are not logically equivalent.
Here are some examples that illustrate how DeMorgan’s laws are used to negate statements involving “and” or “or.”
[latex]R[/latex] : You can solve it by factoring or with the quadratic formula.
[latex]R[/latex] : The numbers [latex]x[/latex] and [latex]y[/latex] are both odd.