Exponential (Population) Growth

Suppose that every year, only [latex]10\%[/latex] of the fish in a lake have surviving offspring. If there were [latex]100[/latex] fish in the lake last year, there would now be [latex]110[/latex] fish. If there were [latex]1000[/latex] fish in the lake last year, there would now be [latex]1100[/latex] fish. Absent any inhibiting factors, populations of people and animals tend to grow by a percent of the existing population each year.

Suppose our lake began with [latex]1000[/latex] fish, and [latex]10\%[/latex] of the fish have surviving offspring each year. Since we start with [latex]1000[/latex] fish, [latex]P_0 = 1000[/latex]. How do we calculate [latex]P_1[/latex]? The new population will be the old population, plus an additional [latex]10\%[/latex]. Symbolically:

[latex]P_{1}=P_{0}+0.10P_{0}[/latex]

representing percent as a decimal

The above statement can be read as “the number of fish in the pond after the first year is equivalent to the initial number of fish plus [latex]10\%[/latex],” where [latex]10\%[/latex] has been expressed in decimal form at [latex]0.10[/latex].

To rewrite a percent as a decimal, drop the [latex]\%[/latex] symbol and move the decimal point two places to the left.

Notice this could be condensed to a shorter form by factoring:

[latex]P_1 = P_0 + 0.10P_0 = 1P_{0} + 0.10P_0 = (1+ 0.10)P_0 = 1.10P_0[/latex]

While [latex]10%[/latex] is the growth rate, [latex]1.10[/latex] is the growth multiplier. Notice that [latex]1.10[/latex] can be thought of as “the original [latex]100\%[/latex] plus an additional [latex]10\%[/latex].”

For our fish population,

[latex]P_1 = 1.10(1000) = 1100[/latex]

We could then calculate the population in later years:

[latex]P_2 = 1.10P_1 = 1.10(1100) = 1210[/latex]

[latex]P_3 = 1.10P_2 = 1.10(1210) = 1331[/latex]

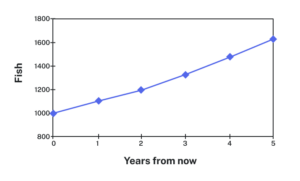
Notice that in the first year, the population grew by [latex]100[/latex] fish; in the second year, the population grew by [latex]110[/latex] fish; and in the third year the population grew by [latex]121[/latex] fish.

While there is a constant percentage growth, the actual increase in number of fish is increasing each year.

Graphing these values we see that this growth doesn’t quite appear linear.

 

A walk-through of this fish scenario can be viewed here:

You can view the transcript for “Exponential Growth Model Part 1” here (opens in new window).

To get a better picture of how this percentage-based growth affects things, we need an explicit form, so we can quickly calculate values further out in the future.

Like we did for the linear model, we will start building from the recursive equation:

[latex]P_1 = 1.10P_0 = 1.10(1000)[/latex]

[latex]P­_2 = 1.10P_1 = 1.10(1.10(1000)) = 1.10^{2}(1000)[/latex]

[latex]P_3 = 1.10P_2 = 1.10(1.102(1000)) = 1.10^{3}(1000)[/latex]

[latex]P_4 = 1.10P_3 = 1.10(1.103(1000)) = 1.10^{4}(1000)[/latex]

Observing a pattern, we can generalize the explicit form to be:

[latex]P_n= 1.10^{n}(1000)[/latex], or equivalently, [latex]P_n = 1000(1.10^{n})[/latex]

From this, we can quickly calculate the number of fish in [latex]10[/latex], [latex]20[/latex], or [latex]30[/latex] years:

 

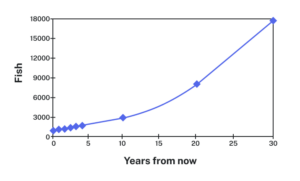
[latex]P_{10}= 1.10^{10}(1000) = 2594[/latex]

[latex]P_{20} = 1.10^{20}(1000) = 6727[/latex]

[latex]P_{30} = 1.10^{30}(1000) = 17449[/latex]

Adding these values to our graph reveals a shape that is definitely not linear. If our fish population had been growing linearly, by [latex]100[/latex] fish each year, the population would have only reached [latex]4000[/latex] in 30 years, compared to almost [latex]18,000[/latex] with this percent-based growth, called exponential growth.

A video demonstrating the explicit model of this fish story can be viewed here:

You can view the transcript for “Exponential Growth Model Part 2” here (opens in new window).