Angle Basics
An angle is formed when two lines, line segments, or rays meet at a common endpoint called the vertex. The two lines or segments that form the angle are called the sides of the angle. Often times you will see an angle denoted by the symbol [latex]\angle[/latex].
Angles are measured either in degrees ([latex]^\circ[/latex]) or radians. We use a protractor to measure the size of an angle.
measure of an angle
The measure of an angle is a numerical value that represents the amount of rotation or separation between two lines or line segments. It quantifies the size of the angle.
We use the abbreviation [latex]m[/latex] to for the measure of an angle. The measure of [latex]\angle A[/latex] is written [latex]m\angle A[/latex].
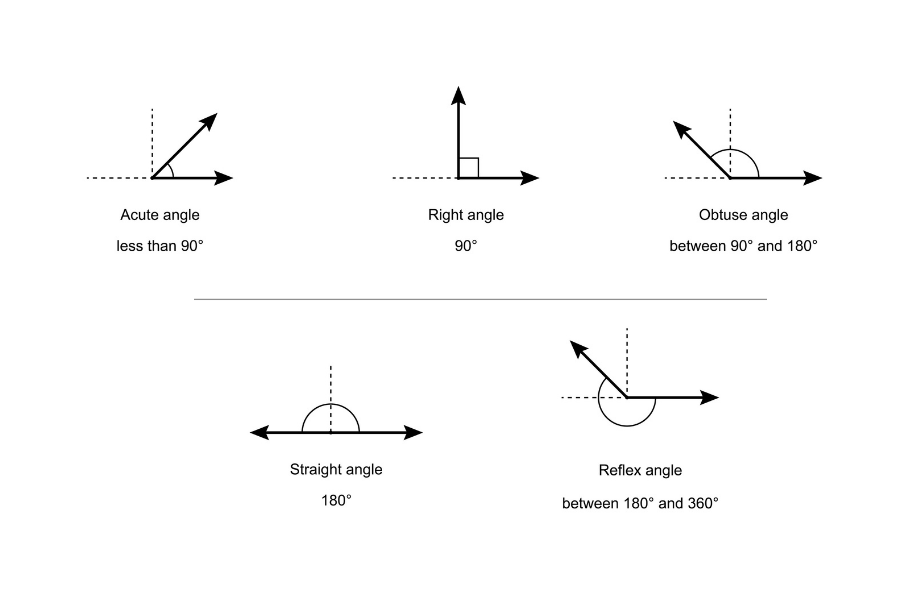
There are five types of angles:
- Right Angle: A right angle measures exactly [latex]90[/latex] degrees. It forms a perfect “L” shape.
- Acute Angle: An acute angle measures less than [latex]90[/latex] degrees. It is smaller than a right angle.
- Obtuse Angle: An obtuse angle measures more than [latex]90[/latex] degrees but less than [latex]180[/latex] degrees. It is larger than a right angle.
- Straight Angle: A straight angle measures exactly [latex]180[/latex] degrees. It forms a straight line.
- Reflex Angle: A reflex angle measures more than [latex]180[/latex] degrees but less than [latex]360[/latex] degrees. It is larger than a straight angle.
angle basics
Angles, symbolized by [latex]\angle[/latex], are formed by the union of two lines, line segments, or rays with a common endpoint, known as a vertex. Angles are measured in either degrees or radians. There are five types of angles.
Measuring Angles
To measure an angle accurately, we use a tool called a protractor. A protractor is a semicircular device with degree markings ranging from [latex]0^\circ[/latex] to [latex]180^\circ[/latex] or [latex]0^\circ[/latex] to [latex]360^\circ[/latex], depending on the type.
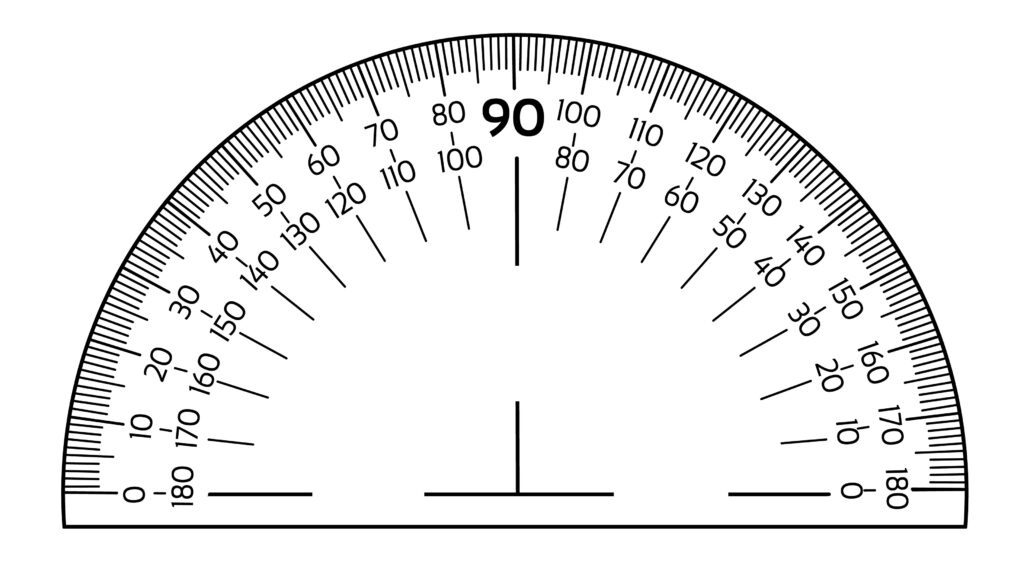
How to: Use a Protractor
- Place the protractor on the vertex (the common endpoint) of the angle, aligning the straight edge of the protractor with one side of the angle. Ensure that the center of the protractor is at the vertex.
- Check the protractor for a zero mark or a baseline that starts at zero. Align the zero mark with the side of the angle that you are measuring from.
- Look at the degree markings on the curved part of the protractor. Read the degree value where the other side of the angle intersects the protractor. This measurement represents the size of the angle in degrees.
When reading the measurement, make sure to align your line of sight parallel to the protractor markings to avoid parallax errors that could affect the accuracy of the measurement. If the angle falls between two degree markings, you can estimate the measurement by observing the position of the intersecting line relative to the markings.
It is important to note a protractor measures angles in degrees. As mentioned before, angles and be measured in either degrees or radians. Let’s explore the difference between these two measurements.
Degrees versus Radians
Degrees are the most common measurement of angles. The symbol for degrees is a small, raised circle: [latex]^\circ[/latex]. A circle is divided into [latex]360^\circ[/latex].
You will use degrees a lot as you learn geometry but you may see it in other areas of life as well. Degrees are used in:
- Navigation – navigation systems, such as compasses and GPS devices, use degrees to indicate directions.
- Construction – degrees are used in construction and engineering to measure and specify angles when building structures. Architects, carpenters, and engineers use degrees to determine the angle of roof slopes, the inclination of ramps, or the angles of intersecting beams.
- Astronomy – astronomers use degrees to describe the positions of celestial objects, angular separations between stars or planets, and the size of apparent motions of celestial bodies.
- Sports – in golf, angles are used to calculate the direction and trajectory of shots. In basketball, the angle of a player’s jump shot can affect the ball’s path to the basket.
- Art and design – when creating perspective drawings or determining the tilt and angles of lines in graphic design, degrees are used to ensure accurate proportions and compositions.
Radians are an alternative unit of angle measurement. Radians are based on the concept of using the radius of a circle to measure angles. In a circle, there are [latex]2π[/latex] radians, where [latex]π[/latex] (pi) is approximately [latex]3.14[/latex]. Radians are considered a more natural unit for measuring angles in mathematics because they directly relate to the geometry of circles. The symbol for radians is [latex]\text{rad}[/latex]. You may not encounter radians unless you plan on exploring advanced mathematics. Radians are often used in advanced mathematical calculations because they provide more precise and convenient measurements when working with trigonometric functions and calculus.
Since there are [latex]360[/latex] degrees in a circle and [latex]2π[/latex] radians in a circle, the conversion factor between degrees and radians is [latex]\frac{180}{π}[/latex]. It is expected to keep the [latex]π[/latex] symbol and not convert to decimal in order to maintain precision.
degrees versus radians
- Degrees are the most common measurement of angles. A circle is divided into [latex]360^\circ[/latex]. The symbol for degrees is a small, raised circle: [latex]^\circ[/latex].
- Radians are an alternative unit of angle measurement. In a circle, there are [latex]2π[/latex] radians, where [latex]π[/latex] (pi) is approximately [latex]3.14[/latex]. The symbol for radians is [latex]\text{rad}[/latex].
The conversion factor between degrees and radians is [latex]\frac{180}{π}[/latex].
[latex]\text{Angle in Degrees} = \text{Angle in Radians }\times\frac{180}{π}[/latex]
[latex]\text{Angle in Radians} = \text{Angle in Degrees }\times\frac{π}{180}[/latex]
Degrees are commonly used in everyday situations like navigation, construction, and basic geometry, while radians are more prevalent in advanced mathematics, physics, engineering, and other scientific fields.