- Identify integers
- Compare positive and negative integers using a number line
- Understand absolute value
- Add, subtract, multiply, and divide integers
Opposites and Integers
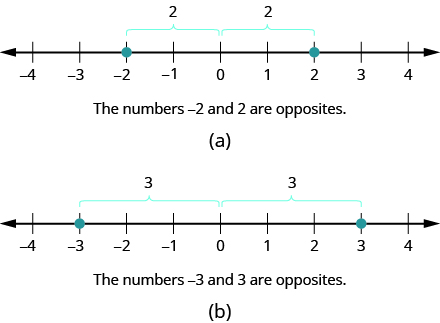
On the number line, the negative numbers are a mirror image of the positive numbers with zero in the middle. Because the numbers [latex]2[/latex] and [latex]-2[/latex] are the same distance from zero, they are called opposites. The opposite of [latex]2[/latex] is [latex]-2[/latex], and the opposite of [latex]-2[/latex] is [latex]2[/latex] as shown in figure(a). Similarly, [latex]3[/latex] and [latex]-3[/latex] are opposites as shown in figure(b).
Opposite
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
The notation [latex]-a[/latex] is read the opposite of [latex]a[/latex].
| [latex]10 - 4[/latex] | Between two numbers, the symbol indicates the operation of subtraction. We read [latex]10 - 4[/latex] as [latex]10[/latex] minus [latex]4[/latex]. |
| [latex]-8[/latex] | In front of a number, the symbol indicates a negative number.We read [latex]-8[/latex] as negative eight. |
| [latex]-x[/latex] | In front of a variable or a number, it indicates the opposite.We read [latex]-x[/latex] as the opposite of [latex]x[/latex] . |
| [latex]-\left(-2\right)[/latex] | Here we have two signs. The sign in the parentheses indicates that the number is negative [latex]2[/latex]. The sign outside the parentheses indicates the opposite. We read [latex]-\left(-2\right)[/latex] as the opposite of [latex]-2[/latex], which is [latex]2[/latex]. |
Integers
Integers are counting numbers, their opposites, and zero.
[latex]\dots{-3,-2,-1,0,1,2,3}\dots[/latex]