Graph Basics

1.  Graph S has [latex]5[/latex] vertices labeled a, b, c, d, and e.
2.  
3.  The vertices are labeled a, b, c, d, e, and the additional vertex f.
4.  
5. Graph T
6.  

Graph Structures

 

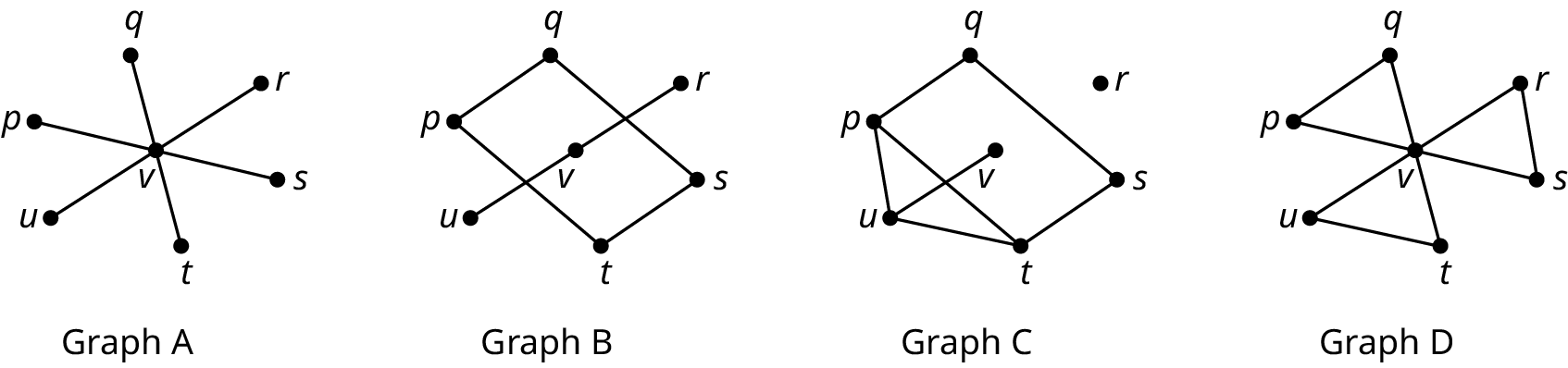
7. Graph B has an edge between vertices v and r that does not exist in Graph C. For B to be a subgraph of C, all of B’s edges would have to be present in C with exactly the same connections between vertices. Since the edge is missing in Graph C, we can conclusively say that Graph B is not a subgraph of Graph C.
8.  

Navigating Graphs

9. The sequence e – d – b – e – f is both a walk and a trail. It is not a path due to the repeated vertex e.
10.  
11. This is not a valid walk, trail, or path. There’s no direct edge from f to b, the sequence e – f – b – d cannot occur without passing through another vertex or edge. 
12.  
13.  The sequence m – n – o – q – n – p – o – n – m is a closed walk because it starts and ends at the same vertex (m) and traverses through edges more than once. It is not a circuit (closed trail) because it uses some edges more than once. It is also not a cycle (closed path) because it revisits vertices.
14.  

Euler Circuits

For the following exercises, use the graphs and multigraphs shown below (Figure 4). Identify any graphs and/or multigraphs with the given characteristics. If there are none, state so.

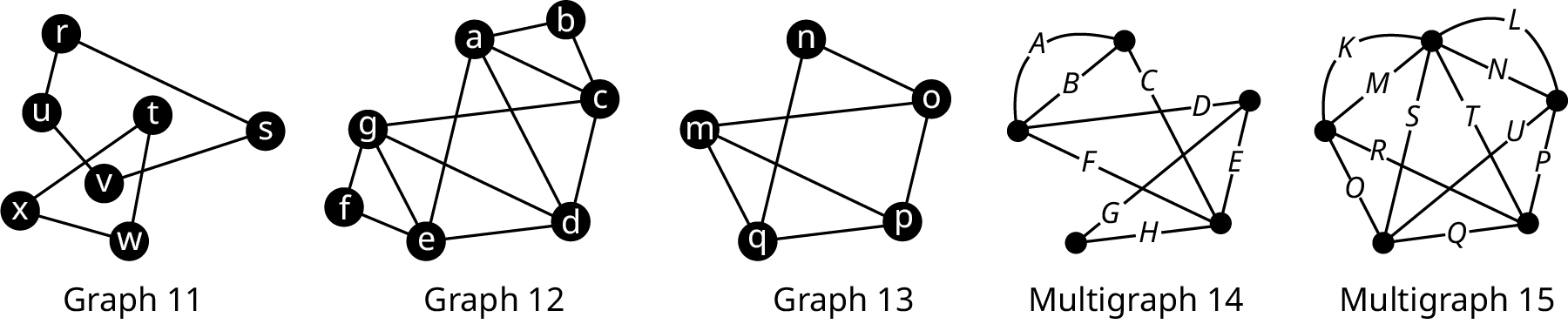
15.  Graphs 11, 12, and 13 are all connected.
16.  
17. Graph 12

Euler Trails

18.  
19. Find an Euler circuit beginning and ending at vertex g in Graph 12 if one exists. Otherwise, explain how you know such an Euler circuit does not exist.
20.  
21. Multigraph 14
22.  

Hamilton Circuits

23. Yes, beginning the Euler trail at vertex d is a good choice, as Fleury’s algorithm requires that for a graph with an Eulerian trail (a trail that visits every edge exactly once), the trail must start (and end) at one of the vertices with an odd degree. The path d→a→b→e→d→f→c→g→f, starts and ends with the vertices that have an odd degree, and does not repeat an edge.
24.  
25. One option is: d→a→b→e→d→f→c→g→f
26.  
27. The sequence m → n → q → o → p → m is a Hamiltonian cycle but not an Eulerian circuit in Graph K.
28.  
29. [latex]39,916,800[/latex]
30.  
31. [latex]239,500,800[/latex]
32.  
33. [latex]70[/latex]

Hamilton Paths

34.  
35. Euler trail
36.  
37. Neither

Traveling Sales Person Problem

42.  
43. The approach described is a brute force algorithm. In a brute force algorithm, all possible solutions are generated and evaluated to find the best solution. In this case, the traveler lists all possible orders in which the cities can be visited, calculates the cost for each possible itinerary, and then selects the one with the least expensive airfare.
44.  
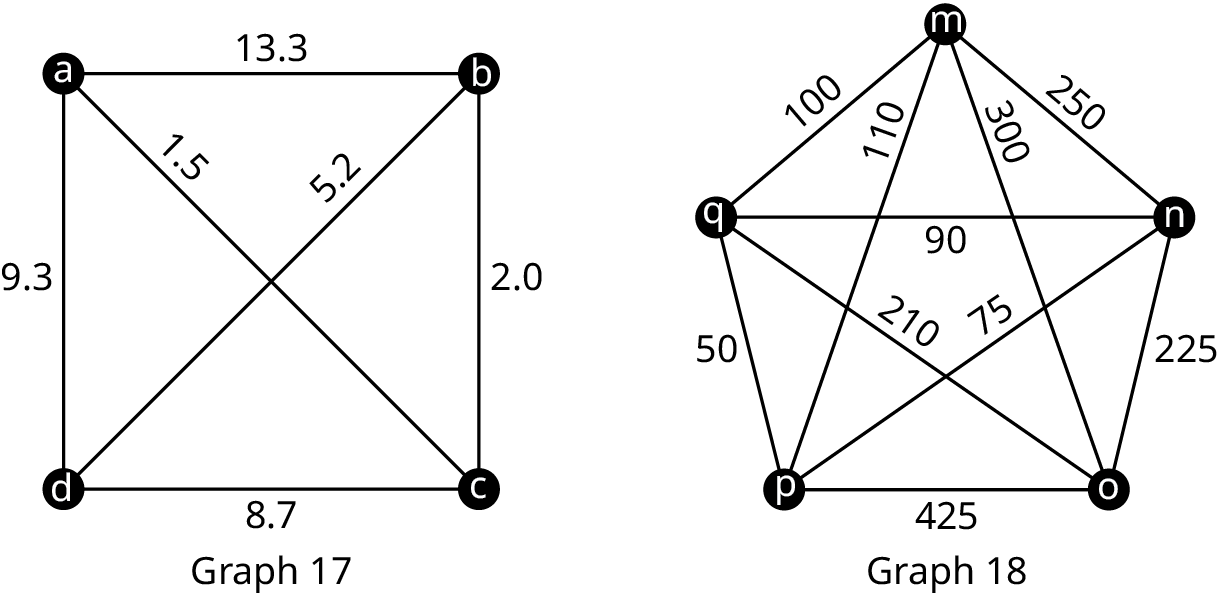
45. The distinct Hamiltonian cycles beginning at vertex ‘m’ in Graph 18, not counting reversals as distinct, are:
    • m → n → o → p → q → m
    • m → n → o → q → p → m
    • m → n → p → o → q → m
    • m → n → p → q → o → m
    • m → n → q → o → p → m
    • m → n → q → p → o → m
    • m → o → n → p → q → m
    • m → o → n → q → p → m
    • m → o → p → n → q → m
    • m → o → p → q → n → m
    • m → o → q → n → p → m
    • m → o → q → p → n → m
    • Note: each cycle can be reversed
46.  
47. Cycles a→c→b→d→a and a→d→b→c→a have the lowest weight of [latex]18[/latex].

Spanning Trees

For the following exercises, draw a graph with the given characteristics.

44.  
45. Answers may very
46.  
47. Answers may very

For the following exercises, use Kruskal’s Algorithm to find a minimum spanning tree of the given graph (figure 12). Graph it and calculate its weight.

48.  
49.