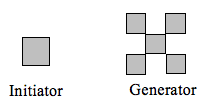
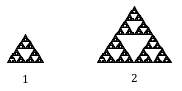Fractal Dimension

In addition to visual self-similarity, fractals exhibit other interesting properties. For example, notice that each step of the Sierpinski gasket iteration removes one quarter of the remaining area. If we remove one quarter of the remaining area indefinitely, we would end up essentially removing all the area on the shape. In other words, we started with a [latex]2[/latex]-dimensional area, and somehow end up with something less than that, but seemingly more than just a [latex]1[/latex]-dimensional line.

To explore this idea, we need to discuss dimension. Something like a line is [latex]1[/latex]-dimensional; it only has length. Any curve is [latex]1[/latex]-dimensional. Things like boxes and circles are [latex]2[/latex]-dimensional, since they have length and width, describing an area. Objects like boxes and cylinders have length, width, and height, describing a volume, and are [latex]3[/latex]-dimensional.

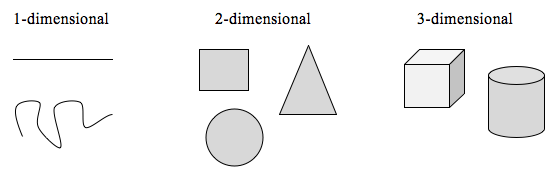
Certain rules apply for scaling objects, related to their dimension.

If we had a line with length [latex]1[/latex], and wanted to scale its length by [latex]2[/latex], we would need two copies of the original line. If we had a line of length [latex]1[/latex], and wanted to scale its length by [latex]3[/latex], we would need three copies of the original.

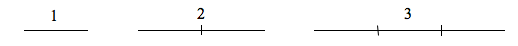
If we had a rectangle with length [latex]2[/latex] and height [latex]1[/latex], and wanted to scale its length and width by [latex]2[/latex], we would need four copies of the original rectangle. If we wanted to scale the length and width by [latex]3[/latex], we would need nine copies of the original rectangle.

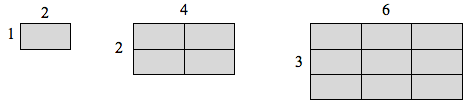
If we had a cubical box with sides of length [latex]1[/latex], and wanted to scale its length and width by [latex]2[/latex], we would need eight copies of the original cube. If we wanted to scale the length and width by [latex]3[/latex], we would need [latex]27[/latex] copies of the original cube.

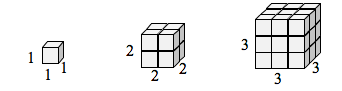
Notice that in the [latex]1[/latex]-dimensional case, copies needed = scale.

In the [latex]2[/latex]-dimensional case, copies needed = scale[latex]^{2}[/latex].

In the [latex]3[/latex]-dimensional case, copies needed = scale[latex]^{3}[/latex].

From these examples, we might infer a pattern.

Use the scaling-dimension relation to determine the dimension of the Sierpinski gasket.

Show Solution

Suppose we define the original gasket to have a side length of [latex]1[/latex]. The larger gasket shown is twice as wide and twice as tall, so has been scaled by a factor of [latex]2[/latex].

 

Notice that to construct the larger gasket, [latex]3[/latex] copies of the original gasket are needed. Using the scaling-dimension relation [latex]C=S^{D}[/latex], we obtain the equation [latex]3=2^{D}[/latex]. Since [latex]2^{1}=2[/latex] and [latex]2^{2}=4[/latex], we can immediately see that [latex]D[/latex] is somewhere between [latex]1[/latex] and [latex]2[/latex]; the gasket is more than a [latex]1[/latex]-dimensional shape, but we’ve taken away so much area it is now less than [latex]2[/latex]-dimensional. Solving the equation [latex]3=2^{D}[/latex] requires logarithms.

If you studied logarithms earlier, you may recall how to solve this equation (if not, just skip to the box below and use that formula with the log key on a calculator):

[latex]3={{2}^{D}}[/latex]	Take the logarithm of both sides.
[latex]\log(3)=\log\left({{2}^{D}}\right)[/latex]	Use the exponent property of logs.
[latex]\log(3)=D\log\left(2\right)[/latex]	Divide by [latex]\log(2)[/latex].
[latex]D=\frac{\log\left(3\right)}{\log(2)}\approx1.585[/latex]	The dimension of the gasket is about [latex]1.585[/latex].

Determine the fractal dimension of the fractal produced using the initiator and generator.

 

Show Solution

 

Scaling the fractal by a factor of [latex]3[/latex] requires [latex]5[/latex] copies of the original.

[latex]D=\frac{\text{log}\left(5\right)}{\text{log}\left(3\right)}\approx1.465[/latex]