Euler and Hamiltonian Paths and Circuits: Learn It 5

Lumen Learning

Euler and Hamiltonian Paths and Circuits: Learn It 5

Spanning Trees

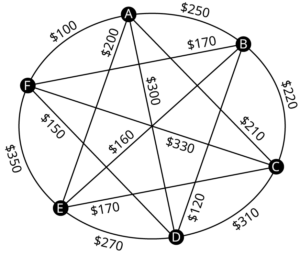
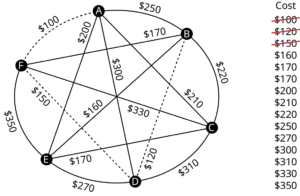
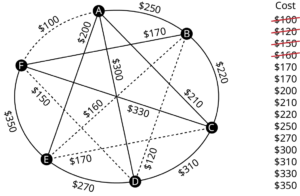
A company requires reliable internet and phone connectivity between their five offices (named [latex]A[/latex], [latex]B[/latex], [latex]C[/latex], [latex]D[/latex], and [latex]E[/latex] for simplicity) in New York, so they decide to lease dedicated lines from the phone company. The phone company will charge for each link made. The costs, in thousands of dollars per year, are shown in the graph.

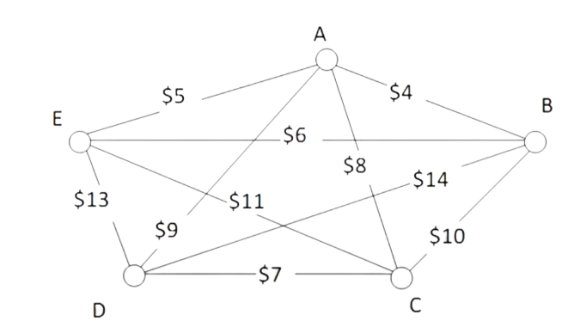
graph with 5 vertices and 11 edges. between A and B is $4, between B and C is $10, between C and D is $7, between D and E is $13, between A and E is $5, between E and B is $6, between E and C is $11, between A and D is $9, between A and C is $8, between B and D is $14.

In this case, we don’t need to find a circuit, or even a specific path; all we need to do is make sure we can make a call from any office to any other. In other words, we need to be sure there is a path from any vertex to any other vertex. We can use a spanning tree.

spanning tree

A spanning tree is a connected graph using all vertices in which there are no circuits.

In other words, there is a path from any vertex to any other vertex, but no circuits.

When deciding whether a graph is a spanning tree, check the following characteristics:

All vertices are included.
No vertices are adjacent that were not adjacent in the original graph.
The graph is connected.
There are no cycles.

Some examples of spanning trees are shown below. Notice there are no circuits in the trees, and it is fine to have vertices with degree higher than two.

Five triangular graphs where there are no Euler circuits, but every vertex has a path to every other vertex.

Use the figure below to determine which of graphs [latex]M1, M2, M3,[/latex] and [latex]M4[/latex], are spanning trees of [latex]Q[/latex].

Five graphs. Graph Q has six vertices: a, b, c, d, e, and f. The edges are a b, a c, a d, b d, d f, c d, c e, c f, and e f. Graph M 1 has six vertices: a, b, c, d, e, and f. The edges are a b, b d, d c, c e, f, and f d. Graph M 2 has six vertices: a, b, c, d, e, and f. The edges are a b, a d, d f, f e, and e c. Graph M 3 has six vertices; a, b, c, d, e, and f. The edges are b d, d f, a f, f e, and e c. Graph M 4 has six vertices: a, b, c, d, e, and f. The edges are a b, c e, e f, and f d.

Usually, we have a starting graph to work from, like in the phone example above. In this case, we form our spanning tree by finding a subgraph – a new graph formed using all the vertices but only some of the edges from the original graph. No edges will be created where they didn’t already exist.

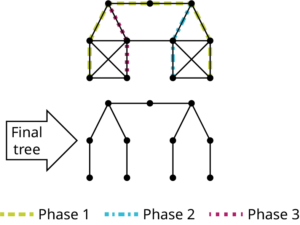
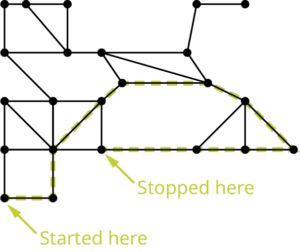
Suppose that you wanted to find a spanning tree within a graph. One approach is to find paths within the graph. You can start at any vertex, go any direction, and create a path through the graph stopping only when you can’t continue without backtracking as shown in the figure below.

A graph with 23 vertices and 35 edges. Ten edges are highlighted in green. Two vertices are labeled started here and stopped here.

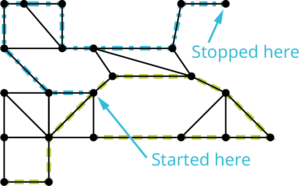
Once you have stopped, pick a vertex along the path you drew as a starting point for another path. Make sure to visit only vertices you have not visited before as shown in the figure below.

A graph with 23 vertices and 35 edges. Ten edges are highlighted in blue. Ten edges are highlighted in green. Two vertices are labeled started here and stopped here.

Repeat this process until all vertices have been visited as shown in the figure below.

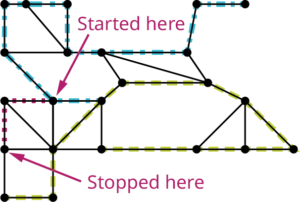
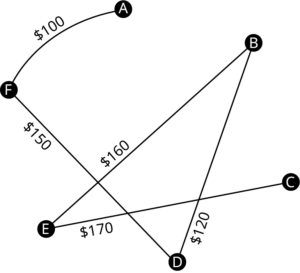
The end result is a tree that spans the entire graph as shown in the figure below.

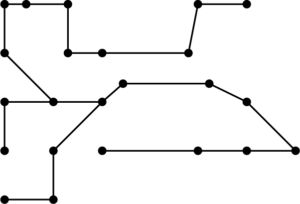
Notice that this subgraph is a tree because it is connected and acyclic. It also visits every vertex of the original graph, so it is a spanning tree. However, it is not the only spanning tree for this graph. By making different turns, we could create any number of distinct spanning trees.

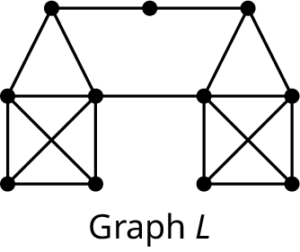
Construct two distinct spanning trees for the graph below.

Graph L has 11 vertices and 19 edges. The graph resembles a square resting below a triangle on either side. The triangles are connected via a trapezoid. The squares have diagonal lines.

Of course, any random spanning tree isn’t really what we want. We want the minimum cost spanning tree (MCST).

In many applications of spanning trees, the graphs are weighted and we want to find the spanning tree of least possible weight. For example, the graph might represent a computer network, and the weights might represent the cost involved in connecting two devices. So, finding a spanning tree with the lowest possible total weight, or minimum spanning tree, means saving money!

minimum cost spanning tree (MCST)

The minimum cost spanning tree is the spanning tree with the smallest total edge weight.

A nearest neighbor style approach doesn’t make as much sense here since we don’t need a circuit, so instead we will take an approach similar to sorted edges.

Kruskal’s algorithm

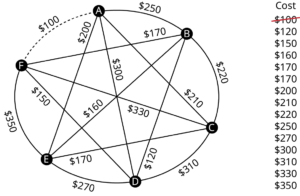
Choose any edge with the minimum weight of all edges.
Choose another edge of minimum weight from the remaining edges. The second edge does not have to be connected to the first edge.
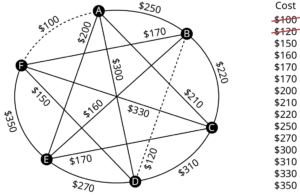
Choose another edge of minimum weight from the remaining edges, but do not select any edge that creates a cycle in the subgraph you are creating.
Repeat step 3 until all the vertices of the original graph are included and you have a spanning tree.

Watch the following video on how to use Kruskal’s Algorithm to find minimum spanning trees.

You can view the transcript for “Use Kruskal’s Algorithm to find Minimum Spanning Trees in Graph Theory” here (opens in new window).

Using our phone line graph from above, begin adding edges:

[latex]\begin{array}{r@{\hfill}l}
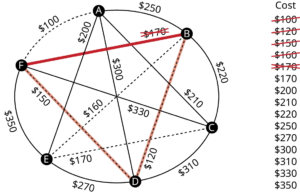
AB && \$4 && \text{OK} \\
AE && \$5 && \text{OK} \\
BE && \$6 && \text{reject – closes circuit ABEA} \\
DC && \$7 && \text{OK} \\
AC && \$8 && \text{OK} \\
\end{array}[/latex]

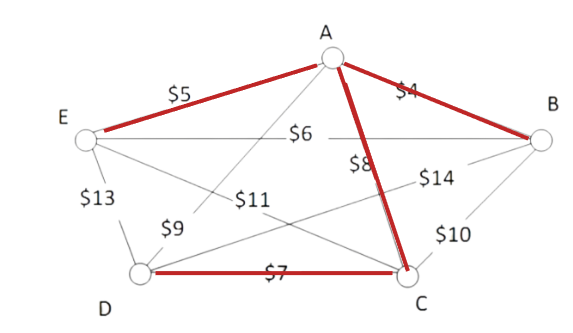
A graph with five vertices labeled A through E. A to B is $4, A to E is $5, B to E is $6, D to C is $7, A to C is $8. AB, AC, AE, and DC are shown in red.

At this point we stop – every vertex is now connected, so we have formed a spanning tree with cost [latex]$24[/latex] thousand a year.

A computer network will be set up with six devices. The vertices in the graph below represent the devices, and the edges represent the cost of a connection. Find the network configuration that will cost the least. What is the total cost?

A graph represents the airfares between six different cities. The graph has 6 vertices. The vertices are A, B, C, D, E, and F. Edges from A leading to B, C, D, E, and F are labeled 250 dollars, 210 dollars, 300 dollars, 200 dollars, and 100 dollars. Edges from B leading to C, D, E, and F are labeled 220 dollars, 120 dollars, 160 dollars, and 170 dollars. Edges from C to D, E, and F are labeled 310 dollars, 180 dollars, and 330 dollars. Edges from D to E and F 270 dollars and 150 dollars. An edge from E to F is labeled 350 dollars.

A minimum spanning tree will correspond to the network configuration of least cost. We will use Kruskal’s algorithm to find one. Since the graph has six vertices, the spanning tree will have six vertices and five edges.

1. Step 1: Choose an edge of least weight. We have sorted the weights into numerical order. The least is [latex]$100[/latex]. The only edge of this weight is edge [latex]AF[/latex] as shown in the figure below.
Step 1 Select Edge [latex]AF[/latex]
1. Step 2: Choose the edge of least weight of the remaining edges, which is [latex]BD[/latex] with [latex]$120[/latex]. Notice that the two selected edges do not need to be adjacent to each other as shown in the figure below.
Step 2 Select Edge [latex]BD[/latex]
1. Step 3: Select the lowest weight edge of the remaining edges, as long as it does not result in a cycle. We select [latex]DF[/latex] with [latex]$150[/latex] since it does not form a cycle as shown in the figure below.

Step 3 Select Edge [latex]DF[/latex]

1. Repeat Step 3: Select the lowest weight edge of the remaining edges, which is [latex]BE[/latex] with [latex]$160[/latex] and it does not form a cycle as shown in figure below. This gives us four edges so we only need to repeat step 3 once more to get the fifth edge.

Repeat Step 3 Select Edge [latex]DF[/latex]

1. Repeat Step 3: The lowest weight of the remaining edges is [latex]$170[/latex]. Both [latex]BF[/latex] and [latex]CE[/latex] have a weight of [latex]$170[/latex], but [latex]BF[/latex] would create cycle ([latex]b, d, f[/latex]) and there cannot be a cycle in a spanning tree as shown in the figure below.

Repeat Step 3 Do Not Select Edge [latex]BF[/latex]

So, we will select [latex]CE[/latex], which will complete the spanning tree as shown in the figure below.

The minimum spanning tree is shown below. This is the configuration of the network of least cost. The spanning tree has a total weight of [latex]$100+$120+$150+$160+$170=$700[/latex], which is the total cost of this network configuration.

Final Minimum Spanning Tree