Hamiltonian Circuits

We just learned how to optimize a walking route for a postal carrier. How is this different than the requirements of a package delivery driver? While the postal carrier needed to walk down every street (edge) to deliver the mail, the package delivery driver instead needs to visit every one of a set of delivery locations. Instead of looking for a circuit that covers every edge once, the package deliverer is interested in a circuit that visits every vertex once.

One Hamiltonian circuit is shown on the graph below. There are several other Hamiltonian circuits possible on this graph. Notice that the circuit only has to visit every vertex once; it does not need to use every edge.

This circuit could be notated by the sequence of vertices visited, starting and ending at the same vertex: [latex]ABFGCDHMLKJEA[/latex]. Notice that the same circuit could be written in reverse order, or starting and ending at a different vertex.

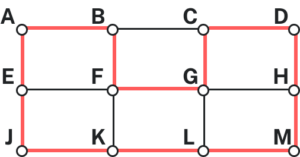
Unlike with Euler circuits, there is no nice theorem that allows us to instantly determine whether or not a Hamiltonian circuit exists for all graphs.^[1]

Does a Hamiltonian circuit exist on the graph below?

Show Solution

We can see that once we travel to vertex [latex]E[/latex] there is no way to leave without returning to [latex]C[/latex], so there is no possibility of a Hamiltonian circuit.

Hamiltonian Paths

Use the graph below to find a Hamilton path between vertices [latex]C[/latex] and [latex]D[/latex].

Show Solution

If we start at vertex [latex]C[/latex], [latex]A[/latex] must be next. Then we must choose between [latex]B[/latex] and [latex]F[/latex]. If we choose [latex]F[/latex], we will have to backtrack to get to include [latex]B[/latex]; so, we must choose [latex]B[/latex]. Once we choose [latex]B[/latex], we must choose [latex]F[/latex] next. After [latex]F[/latex], we choose [latex]E[/latex], because we want to end at [latex]D[/latex]. So, a Hamilton path between [latex]C[/latex] and [latex]D[/latex] is [latex]C → A → B → F → E → D[/latex].

There is not a short way to determine if there is a Hamilton path between two vertices on a graph that works in every situation. However, there are a few common situations that can help us to quickly determine that there is no Hamilton path. Some of these are listed in the table below.

Scenario	Diagram
If an edge [latex]ab[/latex] is a bridge, then there is no Hamilton path between a pair of vertices that are on the same side of edge [latex]ab[/latex].	No Hamilton path between any two vertices in the component [latex]{a, c, d, f}[/latex]. No Hamilton path between any two vertices in [latex]{b, e, h, g, i}[/latex].
If an edge [latex]ab[/latex] is a bridge with at least three components on each side, then there is no Hamilton path beginning or ending at [latex]a[/latex] or [latex]b[/latex].	No Hamilton path beginning or ending at [latex]a[/latex] or [latex]b[/latex].
If a graph is composed of two cycles joined only at a single vertex [latex]p[/latex], and [latex]v[/latex] is any vertex that is NOT adjacent to [latex]p[/latex], then there are no Hamilton paths beginning or ending at [latex]p[/latex].	No Hamilton path can be formed starting or ending at vertices, [latex]r[/latex], [latex]v[/latex], or [latex]u[/latex] because they are not adjacent to [latex]p[/latex].