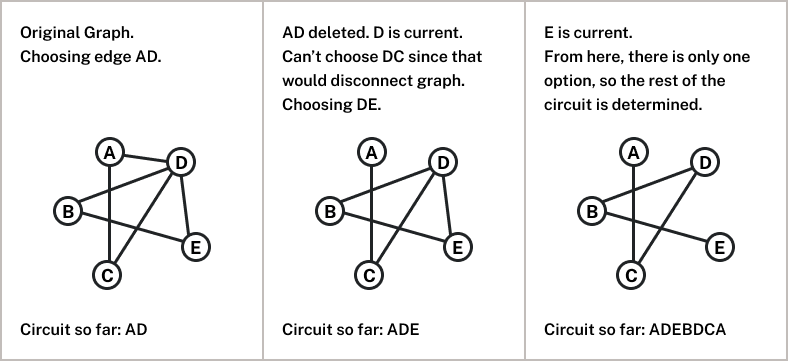
Fleury’s Algorithm
Now we know how to determine if a graph has an Euler circuit, how can we find an Euler circuit in the graph? While it usually is possible to find an Euler circuit just by pulling out your pencil and trying to find one, the more formal method is Fleury’s algorithm.
Fleury’s Algorithm
- Start at any vertex if finding an Euler circuit. If finding an Euler path, start at one of the two vertices with odd degree.
- Choose any edge leaving your current vertex, provided deleting that edge will not separate the graph into two disconnected sets of edges.
- Add that edge to your circuit, and delete it from the graph.
- Continue until you’re done.
The following video presents more examples of using Fleury’s algorithm to find an Euler Circuit.
You can view the transcript for “Graph Theory: Fleury’s Algorthim” here (opens in new window).
Eulerization
Not every graph has an Euler path or circuit. In order to create a Euler circuit on a graph we use a process known as Eulerization .
Eulerization
Eulerization is the process of adding edges to a graph to create an Euler circuit on a graph.
To eulerize a graph, edges are duplicated to connect pairs of vertices with odd degree. Connecting two odd degree vertices increases the degree of each, giving them both even degree. When two odd degree vertices are not directly connected, we can duplicate all edges in a path connecting the two.
Note that we can only duplicate edges, not create edges where there wasn’t one before. Duplicating edges would mean walking or driving down a road twice, while creating an edge where there wasn’t one before is akin to installing a new road!
In the example above, you’ll notice that the last eulerization required duplicating seven edges, while the first two only required duplicating five edges. If we were eulerizing the graph to find a walking path, we would want the eulerization with minimal duplications. If the edges had weights representing distances or costs, then we would want to select the eulerization with the minimal total added weight.
IMPORTANT! Since only duplicate edges can be added to eulerize a graph, it is not possible to eulerize a disconnected graph.
Use Graph [latex]A[/latex] and multigraphs [latex]B, C, D,[/latex] and [latex]E[/latex] given in figure below to answer the questions.
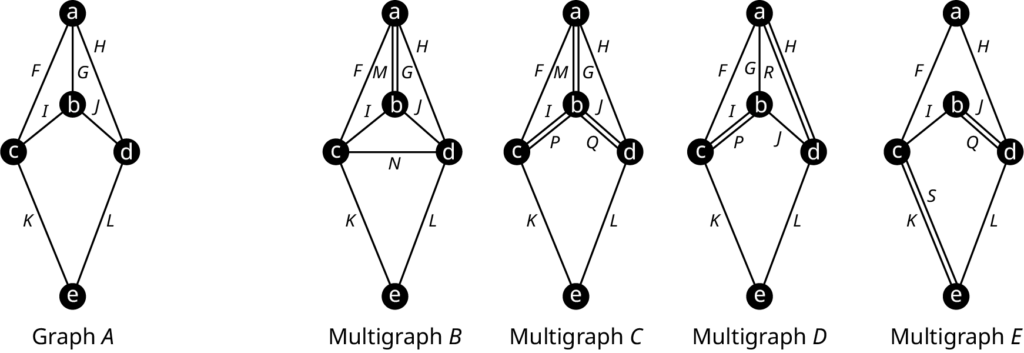
- Which of the multigraphs are not eulerizations of Graph [latex]A[/latex]? Explain your answer.
- Which eulerization of Graph [latex]A[/latex] uses the fewest duplicate edges? How many does it use?
- Is it possible to eulerize Graph [latex]A[/latex] using fewer duplicate edges than your answer to part 2? If so, give an example. If not, explain why not.
It’s important to note that the process of eulerization should respect the rule that only existing edges can be duplicated; new edges cannot be created where there wasn’t one before.
The problem of finding the optimal eulerization is called the Chinese Postman Problem, a name given by an American in honor of the Chinese mathematician Mei-Ko Kwan who first studied the problem in 1962 while trying to find optimal delivery routes for postal carriers. This problem is important in determining efficient routes for garbage trucks, school buses, parking meter checkers, street sweepers, and more.



