- Determine whether a graph has an Euler path or circuit and use Fleury’s algorithm to find an Euler circuit
- Recognize whether a graph contains a Hamiltonian circuit or path and determine the optimal Hamiltonian circuit using various algorithms
- Identify a connected graph as a spanning tree and utilize Kruskal’s algorithm to create both a spanning tree and a minimum-cost spanning tree
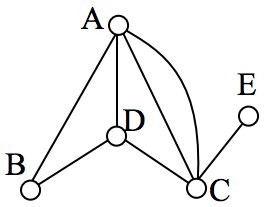
In the first section, we created a graph of the Königsberg bridges and asked whether it was possible to walk across every bridge once. Because Euler first studied this question, these types of paths are named after him.
Euler Circuits
Euler path
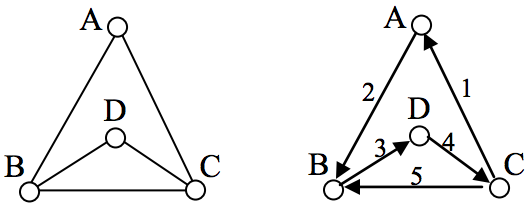
An Euler path is a path that uses every edge in a graph with no repeats. Being a path, it does not have to return to the starting vertex.
Euler circuit
An Euler circuit is a circuit that uses every edge in a graph with no repeats. Being a circuit, it must start and end at the same vertex.
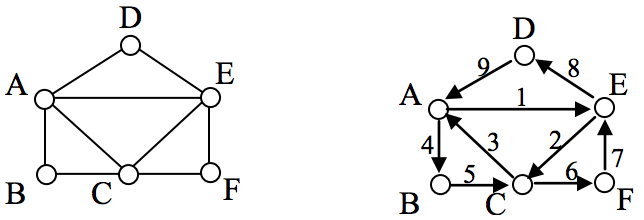
Look back at the example used for Euler paths—does that graph have an Euler circuit? A few tries will tell you no; that graph does not have an Euler circuit. When we were working with shortest paths, we were interested in the optimal path. With Euler paths and circuits, we’re primarily interested in whether an Euler path or circuit exists.
Why do we care if an Euler circuit exists? We care if an Euler circuit exists because it can help us solve problems, such as determining the most efficient route for a traveling salesperson or the optimal path for a network of roads. By finding an Euler circuit, we can ensure that every edge in the graph is visited exactly once, which can help us to avoid redundancy or inefficiency in our solutions. Luckily, Euler solved the question of whether or not an Euler path or circuit will exist.
Euler’s path and circuit theorems
A graph will contain an Euler path if it contains at most two vertices of odd degree.
A graph will contain an Euler circuit if all vertices have even degree