The Inca Counting System

Background

There is generally a lack of books and research material concerning the historical foundations of the Americas. Most of the information available concentrates on the eastern hemisphere, with Europe as the central focus.

The reasons for this may be twofold: first, it is thought that there was a lack of specialized mathematics in the American regions; second, many of the secrets of ancient mathematics in the Americas have been closely guarded.^[1] 

The Peruvian system does not seem to be an exception here. Two researchers, Leland Locke and Erland Nordenskiold, have carried out research that has attempted to discover what mathematical knowledge was known by the Incas and how they used the Peruvian quipu, a counting system using cords and knots, in their mathematics. These researchers have come to certain beliefs about the quipu that we will summarize here.

Counting Boards

It should be noted that the Incas did not have a complicated system of computation. Where other peoples in the regions, such as the Mayans, were doing computations related to their rituals and calendars, the Incas seem to have been more concerned with the simpler task of record-keeping. To do this, they used what are called the “quipu” to record quantities of items. We will explore quipu on the next page. However, they first often needed to do computations whose results would be recorded on quipu.

To do these computations, they would sometimes use a counting board constructed with a slab of stone. In the slab were cut rectangular and square compartments so that an octagonal (eight-sided) region was left in the middle. Two opposite corner rectangles were raised. Another two sections were mounted on the original surface of the slab so that there were actually three levels available. In the figure shown, the darkest shaded corner regions represent the highest, third level. The lighter shaded regions surrounding the corners are the second highest levels, while the clear white rectangles are the compartments cut into the stone slab.

 

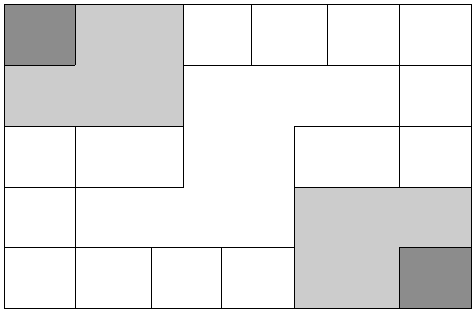
Pebbles were used to keep accounts and their positions within the various levels and compartments gave totals. 

For example, a pebble in a smaller (white) compartment represented one unit. Note that there are [latex]12[/latex] such squares around the outer edge of the figure. If a pebble was put into one of the two (white) larger, rectangular compartments, its value was doubled. When a pebble was put in the octagonal region in the middle of the slab, its value was tripled. If a pebble was placed on the second (shaded) level, its value was multiplied by six. And finally, if a pebble was found on one of the two highest corner levels, its value was multiplied by twelve. Different objects could be counted at the same time by representing different objects by different colored pebbles.

counting boards

Counting boards are ancient tools for arithmetic that use pebbles placed in different sections to represent numbers. The board’s compartments—rectangular, square, and octagonal—multiply the pebbles’ value, enabling complex calculations.

How to: Determine Numbers on a Counting Board

1. Identify the Compartments: Examine the counting board and locate the different compartments—small, rectangular, and octagonal.
2. Recognize the Values: Understand the value each compartment represents: smallest compartments for single units, rectangular spaces for doubled value, and octagonal spaces for tripled value. Pebbles in the shaded second-level compartments have their values multiplied by six, while those on the highest level—the corner spaces—have their values multiplied by twelve.
3. Calculate the Sums: Count the number of pebbles in each compartment and multiply by the compartment’s value.
4. Aggregate the Totals: Add the calculated sums from all compartments together.
5. Interpret the Number: The aggregate total from all compartments represents the number determined by the counting board.

---