- Add, subtract, multiple and divide fractions
- Solve real-world problems using arithmetic with rational functions
- Convert between improper fractions and mixed numbers
Adding and Subtracting Rational Numbers
Adding and subtracting rational numbers isn’t just about combining numbers; it’s about understanding the common ground between them. If the two fractions you are adding have the same denominator or a common denominator, adding or subtracting the two fractions is pretty straightforward.
Adding/Subtracting rational numbers with a common denominator: Add or subtract the numerators, and then place that value in the numerator and the common denominator in the denominator.
If [latex]c[/latex] is a non-zero integer, then [latex]\frac{a}{c} \pm \frac{b}{c}=\frac{a \pm b}{c}[/latex]
Adding and subtracting fractions may seem like a straightforward task, but what happens when the denominators are different? That’s where the concept of the Least Common Multiple (LCM) comes into play.
Finding the least common multiple through prime factorization:
- Find the prime factors of each denominator. You can use a factor tree or division method to break down each number into its prime factors.
- List down all the unique prime factors that appear in the prime factorization of each number.
- For each unique prime factor, identify the highest power to which it is raised in any of the given numbers.
- Multiply together the highest powers of all the unique prime factors. The result is the least common multiple (LCM) of the given numbers.
Once you have found the least common multiple, adding or subtracting fractions with unlike denominators becomes more straightforward.
Adding/Subtracting rational numbers with unlike denominators:
- Find a common denominator using one of the two methods given above.
- Rewrite each fraction using the common denominator.
- Now that the fractions have a common denominator, you can add/subtract the numerators.
- Simplify by canceling out all common factors in the numerator and denominator.
The following video goes into more detail of adding fractions with common denominators.
You can view the transcript for “Adding Fractions with Common Denominators (Step by Step) | Math with Mr. J” here (opens in new window).
The following video goes into more detail of subtracting fractions with common denominators.
You can view the transcript for “Subtracting Fractions with Common Denominators (Step by Step) | Math with Mr. J” here (opens in new window).
Watch the following video to learn why we need a common denominator when adding and subtracting fractions.
You can view the transcript for “Why Do We Need a Common Denominator When Adding and Subtracting Fractions? | Math with Mr. J” here (opens in new window).
The following video explains finding the least common denominator.
You can view the transcript for “Math Antics – Common Denominator LCD” here (opens in new window).
The following video takes another look at prime factorization.
You can view the transcript for “Prime Factorization | Math with Mr. J” here (opens in new window).
In the following video you will see examples of how to add and subtract fractions with different denominators.
You can view the transcript for “Ex: Add and Subtract Fractions with Unlike Denominators (Basic)” here (opens in new window).
Multiplying Rational Numbers
A model may help you understand multiplication of rational numbers. When you multiply a fraction by a fraction, you are finding a “fraction of a fraction.” Suppose you have [latex]\frac{3}{4}[/latex] of a candy bar and you want to find [latex]\frac{1}{2}[/latex] of the [latex]\frac{3}{4}[/latex]:
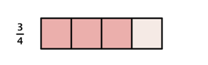
By dividing each fourth in half, you can divide the candy bar into eighths.

Then, choose half of those to get [latex]\frac{3}{8}[/latex].

In both of the above cases, to find the answer, you can multiply the numerators together and the denominators together.
Multiplying rational numbers:
Watch the following video for more examples of multiplying rational numbers.
You can view the transcript for “Ex 2: Multiply Fractions” here (opens in new window).
Dividing Rational Numbers
Just like with multiplying rational numbers, a model may help you understand dividing rational numbers. Suppose you have a pizza that is already cut into 4 slices. How many [latex]\frac{1}{2}[/latex] slices are there?
 |
 |
Figure 4. The slices are divided into halves, turning quarters into eighths
There are [latex]8[/latex] slices. You can see that dividing [latex]4[/latex] by [latex]\frac{1}{2}[/latex] gives the same result as multiplying [latex]4[/latex] by [latex]2[/latex]. What would happen if you needed to divide each slice into thirds?
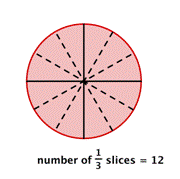
You would have [latex]12[/latex] slices, which is the same as multiplying [latex]4[/latex] by [latex]3[/latex].
Dividing with rational numbers
- Find the reciprocal of the number that follows the division symbol.
- Multiply the first number (the one before the division symbol) by the reciprocal of the second number (the one after the division symbol).
Watch the following video for more examples of dividing rational numbers.
You can view the transcript for “Ex 3: Divide Fractions” here (opens in new window).
Solving Problems Involving Rational Numbers
Watch the following for more examples of determining a fraction of a large whole number.
You can view the transcript for “Determine a Fraction of a Large Whole Number” here (opens in new window).
Converting Between Improper Fractions and Mixed Numbers
Convert an improper fraction to a mixed number.
- Divide the denominator into the numerator.
- Identify the quotient, remainder, and divisor.
- Write the mixed number as quotient [latex]{\Large\frac{\text{remainder}}{\text{divisor}}}[/latex] .
Convert a mixed number to an improper fraction.
- Multiply the whole number by the denominator.
- Add the numerator to the product found in Step 1.
- Write the final sum over the original denominator.
A quotient is the result obtained when one number is divided by another; a remainder is the amount left over after division when the dividend cannot be evenly divided by the divisor; and a divisor is the number by which another number (the dividend) is divided.
Rewrite [latex]\frac{95}{26}[/latex] as a mixed number.
Now you can watch worked examples of how to convert an improper fraction to a mixed number in the following video.
You can view the transcript for “Examples: Convert an Improper Fraction to a Mixed Number” here (opens in new window).
Rewrite [latex]9\frac{5}{14}[/latex] as an improper fraction.
In the following video we show more example of how to convert a mixed number to an improper fraction.
You can view the transcript for “Examples: Converting a Mixed Number to an Improper Fraction” here (opens in new window).