Analyzing Arguments with Venn/Euler Diagrams
We can interpret a deductive argument visually with an Euler diagram, which is essentially the same thing as a Venn diagram. This can make it easier to determine whether the argument is valid or invalid.
How To: Analyzing arguments with Venn/Euler diagrams
- Draw a Venn/ Euler diagram based on the premises of the argument.
- If the premises are insufficient to determine what determines the location of an element, indicate that.
- The argument is valid if it is clear that the conclusion must be true.
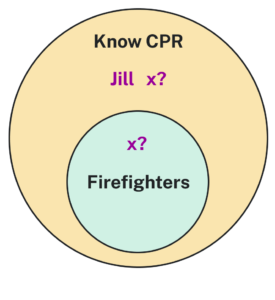
| Premise: | All firefighters know CPR |
| Premise: | Jill knows CPR |
| Conclusion: | Jill is a firefighter |
In addition to these categorical style premises of the form “all ___,” “some ____,” and “no ____,” it is also common to see premises that are implications.
Analyzing Arguments with Truth Tables
Some arguments are better analyzed using truth tables.
How To: Analyzing Arguments Using Truth Tables
- Represent each of the premises symbolically.
- Create a conditional statement, joining all the premises with and to form the antecedent, and using the conclusion as the consequent.
- Create a truth table for that statement. If it is always true, then the argument is valid.
| Premise: | If I go to the mall, then I’ll buy new jeans. |
| Premise: | If I buy new jeans, I’ll buy a shirt to go with it. |
| Conclusion: | If I got to the mall, I’ll buy a shirt. |
The previous problem is an example of a syllogism.
Syllogism
A syllogism is an implication derived from two others, where the consequence of one is the antecedent to the other. The general form of a syllogism is:
| Premise: | [latex]p{\rightarrow}q[/latex] |
| Premise: | [latex]q{\rightarrow}r[/latex] |
| Conclusion: | [latex]p{\rightarrow}r[/latex] |
This is sometimes called the transitive property for implication.
Logical Inference
Suppose we know that a statement of the form [latex]P{\rightarrow}Q[/latex] is true. This tells us that whenever [latex]P[/latex] is true, [latex]Q[/latex] will also be true. By itself, [latex]P{\rightarrow}Q[/latex] being true does not tell us that either [latex]P[/latex] or [latex]Q[/latex] is true (they could both be false or [latex]P[/latex] could be false and [latex]Q[/latex] true). However if in addition, we happen to know that [latex]P[/latex] is true then it must be that [latex]Q[/latex] is true.
This is called a logical inference: Given two true statements, we can infer that a third statement is true. In this instance true statements [latex]P{\rightarrow}Q[/latex] and [latex]P[/latex] are “added together” to get [latex]Q[/latex]. This is described below with [latex]P{\rightarrow}Q[/latex] stacked one atop the other with a line separating them from [latex]Q[/latex]. The intended meaning is that [latex]P{\rightarrow}Q[/latex] combined with [latex]P[/latex] produces [latex]Q[/latex].

Two other logical inferences are listed above. In each case, you should convince yourself (based on your knowledge of the relevant truth tables) that the truth of the statements above the line forces the statement below the line to be true.
Logical inference
Logical inference refers to the process of deriving new knowledge or conclusions based on existing knowledge or premises.
Thus, logic helps us understand the meanings of statements and it also produces new meaningful statements. Logic is the glue that holds strings of statements together and pins down the exact meaning of certain key phrases such as the “If…, then” or “For all” constructions. Logic is the common language that all mathematicians use, so we must have a firm grip on it in order to write and understand mathematics.