Square Roots for Non-Perfect Square Numbers
One collection of irrational numbers is square roots of numbers that aren’t perfect squares. Recall that, [latex]x[/latex] is the square root of the number [latex]a[/latex], denoted [latex]\sqrt{a}[/latex], if [latex]x^2=a[/latex]. The number [latex]a[/latex] is the perfect square of the integer [latex]n[/latex] if [latex]a=n^2[/latex].
perfect square
Perfect squares are integers that result from squaring a whole number.
Square Root Notation
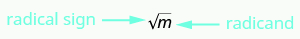
The rational number [latex]\frac{a}{b}[/latex] is a perfect square if both [latex]a[/latex] and [latex]b[/latex] are perfect squares.
One method of determining if an integer is a perfect square is to examine its prime factorization. If, in that factorization, all the prime factors are raised to even powers, the integer is a perfect square.
Another method is to attempt to factor the integer into an integer squared. It is possible that you recognize the number as a perfect square (such as [latex]4[/latex] or [latex]9[/latex]). Or, if you have a calculator at hand, use the calculator to determine if the square root of the integer is an integer.
Determine which of the following are perfect squares.
- [latex]45[/latex]
- [latex]81[/latex]
- [latex]\frac{9}{28}[/latex]
- [latex]\frac{144}{400}[/latex]
Using Desmos to Determine if a Number Is a Perfect Square
Desmos may be used to determine if a number is a perfect square by using its square root function. When Desmos is opened, there is a tab in the lower left-hand corner of the Desmos screen. This tab opens the Desmos keypad, shown below.

There you find the key for the square root, which is circled in the image above. To find the square root of a number, click the square root key, which begins a calculation, and then enter the value for which you want a square root. If the result is an integer, then the number is a perfect square. For more information on this, watch this video on Using Desmos to Find the Square Root of a Number.
You can view the transcript for “Square Roots on Desmos Calculator” here (opens in new window).
Square roots of perfect squares are always whole numbers, so they are rational. But the decimal forms of square roots of numbers that are not perfect squares never stop and never repeat, so these square roots are irrational.
square roots of non perfect squares
The decimal forms of square roots of numbers that are not perfect squares never stop and never repeat, so these square roots are irrational.
- [latex]\sqrt{36}[/latex]
- [latex]\sqrt{44}[/latex]