Graph Basics

For the following exercises, use the given figure below (Figure 1).

1. Determine the number of vertices in Graph S.
2. Identify the graph with the fewest edges.
3. Name the vertices in Graph U.
4. Identify any pairs of vertices in Graph S that are not adjacent.
5. Which graphs only has vertices of degree 2?
6. Identify the graph in which the sum of the degrees of the vertices is 16.

Graph Structures

For the following exercises, use the given figure below (Figure 2).

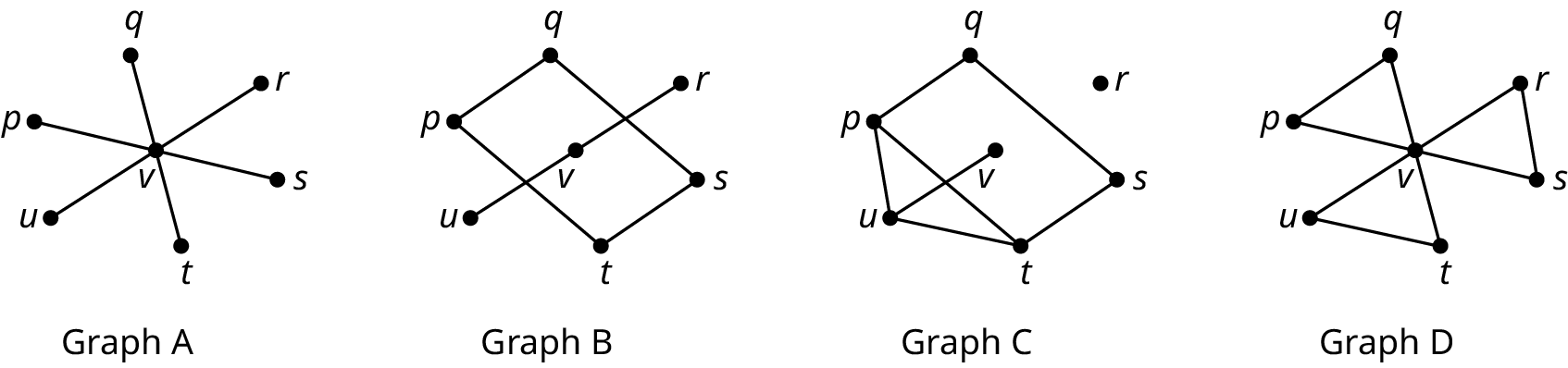
7. Explain why Graph B is not a subgraph of Graph C.
8. How many edges are in a complete graph with 12 vertices?

Navigating Graphs

For the following exercises, use Graph A in the given figure below (Figure 3). Consider each sequence of vertices. Determine if it is only a walk, both a walk and a path, both a walk and a trail, all three, or none of these.

9. e → d → b → e → f
10. e → b → d → e → f → c → b → d
11. e → f → b → d

For the following exercises, use Graph K (Figure 3) . Identify each sequence of vertices as a closed walk, circuit (closed trail), and/or directed cycle (closed path). Indicate all that apply.

12. n → o → q → n → p → m → n
13. m → n → o → q → n → p → o → n → m
14. p → o → q → n → m → p

Euler Circuits

For the following exercises, use the graphs and multigraphs shown below (Figure 4). Identify any graphs and/or multigraphs with the given characteristics. If there are none, state so.

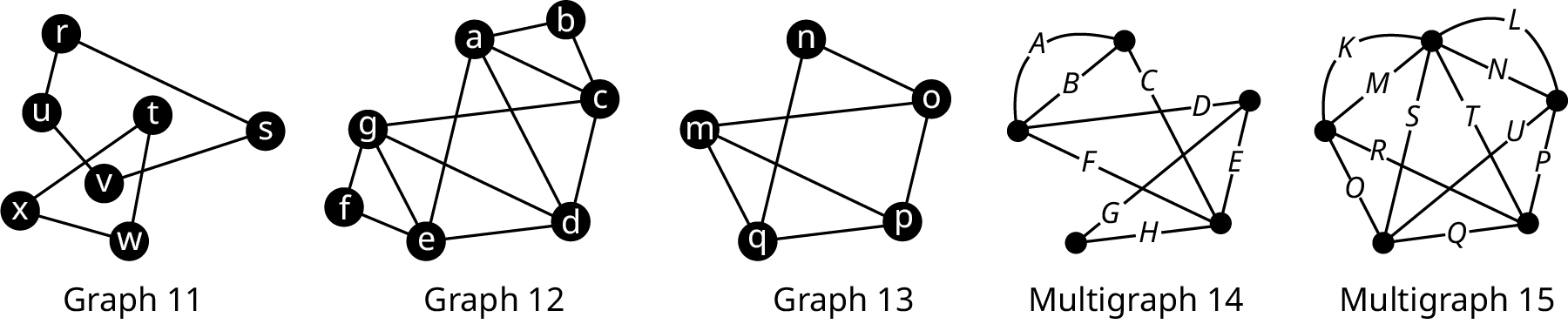
15. connected
16. disconnected
17. Eulerian

Euler Trails

For the following exercises, use the graphs and multigraphs in Figure 4.

18. Determine whether the sequence of edges represents an Euler circuit in Multigraph 15: K → L → N → M → O → S → T → Q → U → P → R
19. Find an Euler circuit beginning and ending at vertex g in Graph 12 if one exists. Otherwise, explain how you know such an Euler circuit does not exist.
20. Give an example of a pair of edges that could be duplicated to eulerize Multigraph 14.

For the following exercises, use the graphs and multigraphs in Figure 4. Identify any graphs and/or multigraphs with the given characteristics. If there are none, state so.

21. Exactly two vertices of odd degree
22. Has an Euler trail

Hamilton Circuits

For the following exercises, refer to the graph in the given in figure 5.

23. A student has been asked to use Fleury’s algorithm to construct an Euler trail in the given graph. The student decides to begin the trail at vertex d. Is this a good choice, why or why not?
24. A student who is using Fleury’s algorithm to construct an Euler trail has decided to begin with f → d → a → b → …. If the student is off to a good start, help the student by completing the Euler trail. If the student has made an error, explain the error.
25. Use Fleury’s algorithm to construct an Euler trail for the given graph beginning at the vertex of your choice.

For the following exercises, use the graphs from figures 6 and 7 to determine whether the sequence of vertices in the given graph is a Hamilton cycle, an Euler circuit, both, or neither.

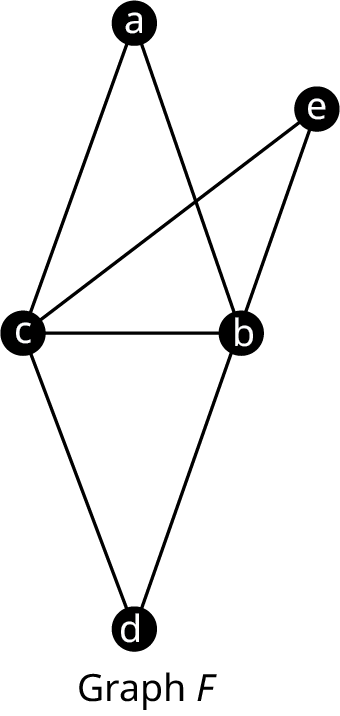
26. Graph F. a → b → e → c → b → d → c → a
27. Graph K. m → n → q → o → p → m
28. Graph A. b → d → e → f → c → b → e

For the following exercises, evaluate the factorial expression for the given value of [latex]n[/latex].

29. [latex](n−1)!,n=12[/latex]
30. [latex](n−1)!,n=14[/latex]
31. Calculate the number of distinct Hamilton cycles in a complete graph with [latex]13[/latex] vertices.

For the following exercises, use figure 8 to find the weight of each Hamilton cycle.

32. q → t → w → x → u → y → v → s → r → q
33. w → x → y → u → v → s → r → q → t → w

Hamilton Paths

For the following exercises, use figure 9 to determine whether the sequence of vertices in the given graph is a Hamilton path, an Euler trail, both, or neither.

34. Graph A. e → b → c → f → e → b → e
35. Graph A. b → c → f → e → d → b → e
36. Graph K. n → q → o → p → m
37. Graph K. o → q → m → n → p

Traveling Sales Person Problem

For the following exercises, determine whether the algorithm described is a greedy algorithm or a brute force algorithm.

38. A lumber distributor is loading pallets onto trucks with the intention of using the fewest trucks possible to send a shipment. The distributor loads the pallets with the greatest length that will fit on the truck first and continues loading until no more pallets will fit. Then the next truck is loaded using the same approach.
39. A traveler wants to visit five cities by airplane. The traveler lists all the possible orders in which the cities can be visited then calculates the best airfare for each itinerary and selects the least expensive option.

For the following exercises, list all the distinct Hamilton cycles beginning at the given vertex in the given graph (figure 10). Indicate which pairs of Hamilton cycles are reverses of each other.

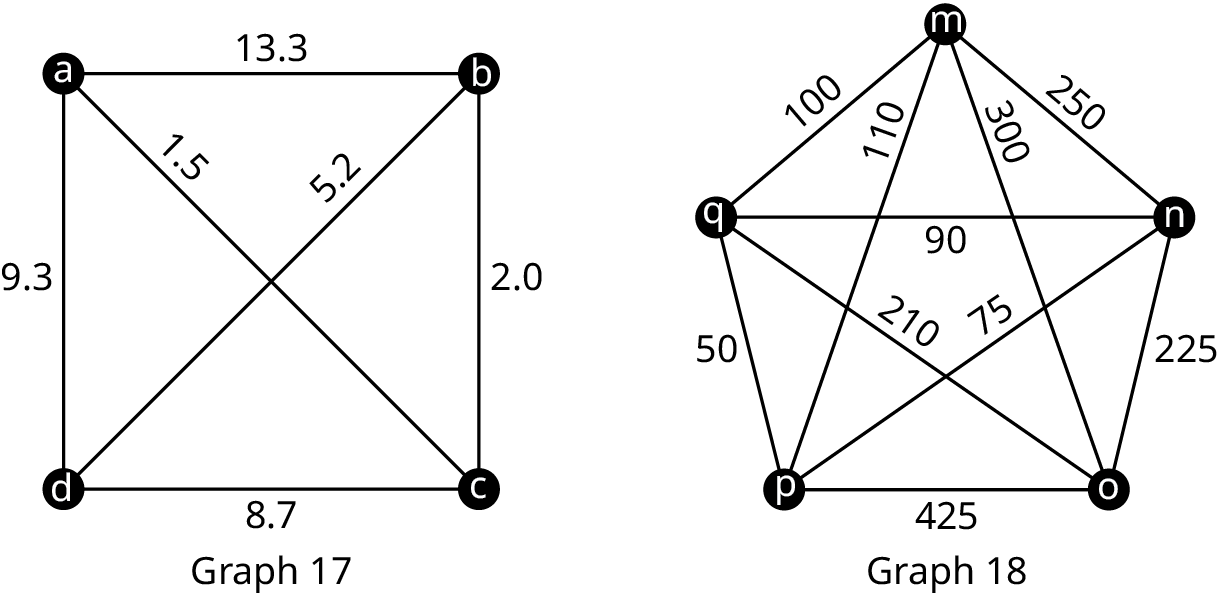
40. Graph 17, vertex a
41. Graph 18, vertex m

For the following exercises, find a Hamilton cycle of least weight for the given graph in Figure 10, beginning at the given vertex, and using the brute force method. What is the weight of the cycle?

42. Graph 18; vertex m
43. Graph 17; vertex a

Spanning Trees

For the following exercises, draw a graph with the given characteristics.

44. A tree with eight vertices, exactly two of degree three.
45. A connected graph with eight vertices, exactly two of degree 3, which is not a tree.

For the following exercises, use figure 11 to draw three possible spanning trees that fit the given description.

46. Three spanning trees of Graph A, which include both edges be and de.
47. Three spanning trees of Graph K, which include edges mn and oq, but do not include no.

For the following exercises, use Kruskal’s Algorithm to find a minimum spanning tree of the given graph (figure 12). Graph it and calculate its weight.

48. Graph 17
49. Graph 18