- Recognize different number types, such as whole numbers, integers, and counting numbers
Identify Counting Numbers and Whole Numbers
In elementary mathematics, we frequently use the most fundamental set of numbers, which we typically employ for counting objects: [latex]1, 2, 3, 4, 5, ...[/latex] and so forth. These numbers are referred to as the counting numbers.
The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called the whole numbers.
Whole and Counting Numbers
Counting numbers start with [latex]1[/latex] and continue.
[latex]1,2,3,4,5\dots[/latex]
Whole numbers are the counting numbers and zero.
[latex]0,1,2,3,4,5\dots[/latex]
Opposites and Integers
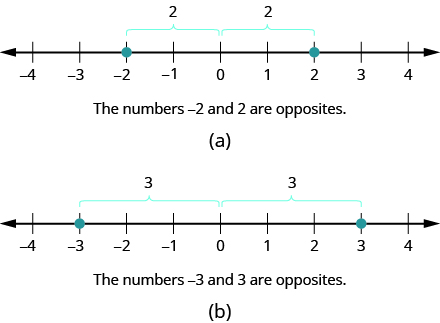
On the number line, the negative numbers are a mirror image of the positive numbers with zero in the middle. Because the numbers [latex]2[/latex] and [latex]-2[/latex] are the same distance from zero, they are called opposites. The opposite of [latex]2[/latex] is [latex]-2[/latex], and the opposite of [latex]-2[/latex] is [latex]2[/latex] as shown in figure(a). Similarly, [latex]3[/latex] and [latex]-3[/latex] are opposites as shown in figure(b).
Opposite
The opposite of a number is the number that is the same distance from zero on the number line but on the opposite side of zero.
The notation [latex]-a[/latex] is read the opposite of [latex]a[/latex].
| [latex]10 - 4[/latex] | Between two numbers, the symbol indicates the operation of subtraction.We read [latex]10 - 4[/latex] as [latex]10[/latex] minus [latex]4[/latex] . |
| [latex]-8[/latex] | In front of a number, the symbol indicates a negative number.We read [latex]-8[/latex] as negative eight. |
| [latex]-x[/latex] | In front of a variable or a number, it indicates the opposite.We read [latex]-x[/latex] as the opposite of [latex]x[/latex] . |
| [latex]-\left(-2\right)[/latex] | Here we have two signs. The sign in the parentheses indicates that the number is negative [latex]2[/latex]. The sign outside the parentheses indicates the opposite.We read [latex]-\left(-2\right)[/latex] as the opposite of [latex]-2[/latex], which is [latex]2[/latex]. |
Integers
Integers are counting numbers, their opposites, and zero.
[latex]\dots{-3,-2,-1,0,1,2,3}\dots[/latex]