- Add, subtract, multiple and divide fractions
- Solve real-world problems using arithmetic with rational functions
- Convert between improper fractions and mixed numbers
- product: the result of multiplication
- factor: something being multiplied – for [latex]3 \cdot 2 = 6[/latex] , both 3 and 2 are factors of 6
- numerator: the top part of a fraction – the numerator in the fraction [latex]\frac{2}{3}[/latex] is 2
- denominator: the bottom part of a fraction – the denominator in the fraction [latex]\frac{2}{3}[/latex] is 3
Adding Rational Numbers
The first step in adding rational numbers is to check if they have the same bottom number, also known as a ‘common denominator.’ When the two rational numbers have a common denominator, then adding the two numbers is straightforward.
adding rational numbers with a common denominator
Add the numerators, and then place that value in the numerator and the common denominator in the denominator.
Symbolically, we write this as: If [latex]c[/latex] is a non-zero integer, then [latex]\frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}[/latex]
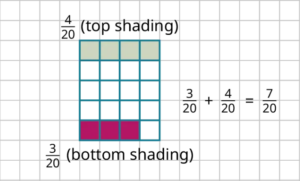
The image below shows the addition of [latex]\frac{3}{20}+\frac{4}{20}=\frac{7}{20}[/latex].
Many different words are used by math textbooks and teachers to provide students with instructions on what they are to do with a given problem. For example, you may see instructions such as “Find” or “Simplify” in the example in this module. It is important to understand what these words mean so you can successfully work through the problems in this course.
Here is a short list of the words you may see that can help you know how to work through the problems in this module.
| Instruction | Interpretation |
|---|---|
| Find | Perform the indicated mathematical operations which may include addition, subtraction, multiplication, division. |
| Simplify |
Perform the indicated mathematical operations including addition, subtraction, multiplication, division OR Write a mathematical statement in smallest terms so there are no other mathematical operations that can be performed—often found in problems related to fractions and the order of operations |
| Evaluate | Perform the indicated mathematical operations including addition, subtraction, multiplication, division |
| Reduce | Write a mathematical statement in smallest or lowest terms so there are no other mathematical operations that can be performed—often found in problems related to fractions or division |
| Calculate | Determine the numerical result of a mathematical operation, which may encompass addition, subtraction, multiplication, division, or more complex mathematical procedures |
When the rational numbers do not have common denominators, then we have to transform the rational numbers so that they do have common denominators. This is technically called finding the least common multiple (LCM).
One way to find the least common multiple of two or more numbers is to first multiply each by [latex]1, 2, 3, 4,[/latex] etc.
Find the least common multiple of [latex]2[/latex] and [latex]5[/latex].
| First, list all the multiples of [latex]2[/latex]: | Then list all the multiples of [latex]5[/latex]: |
| [latex]2\cdot 1 = 2[/latex] | [latex]5\cdot 1 = 5[/latex] |
| [latex]2\cdot 2 = 4[/latex] | [latex]5\cdot 2 = 10[/latex] |
| [latex]2\cdot 3 = 6[/latex] | [latex]5\cdot 3 = 15[/latex] |
| [latex]2\cdot 4 = 8[/latex] | [latex]5\cdot 4 = 20[/latex] |
| [latex]2\cdot 5 = 10[/latex] | [latex]5\cdot 5 = 25[/latex] |
The smallest multiple they have in common will be the common denominator for the two! In this case, the LCM would be [latex]10[/latex].
Another method than can be used to find the least common multiple is the prime factorization method.
How To: Finding the Least Common Multiple Through Prime Factorization
- Find the prime factors of each denominator. You can use a factor tree or division method to break down each number into its prime factors.
- List down all the unique prime factors that appear in the prime factorization of each number.
- For each unique prime factor, identify the highest power to which it is raised in any of the given numbers.
- Multiply together the highest powers of all the unique prime factors. The result is the least common multiple (LCM) of the given numbers.
Now that we know how to find the least common multiple, adding fractions with unlike denominators becomes easier.
How To: Adding Rational Numbers With Unlike Denominators
- Find a common denominator.
- Rewrite each fraction using the common denominator.
- Now that the fractions have a common denominator, you can add the numerators.
- Simplify by canceling out all common factors in the numerator and denominator.
Calculate [latex]\frac{11}{18}+\frac{2}{15}[/latex].
Adding Rational Numbers Using a Calculator
Adding rational numbers can be done with a calculator, which often returns a decimal representation, or by finding a common denominator for the rational numbers being added.
Using Desmos to Add Rational Numbers in Fractional Form
To create a fraction in Desmos, enter the numerator, then use the division key (/) on your keyboard, and then enter the denominator. The fraction is then entered. Then click the right arrow key to exit the denominator of the fraction. Next, enter the arithmetic operation (+ or –). Then enter the next fraction. The answer is displayed dynamically (calculates as you enter). To change the Desmos result from decimal form to fractional form, use the fraction button (see image below) on the left of the line that contains the calculation:
