Set Theory
- List out the elements of the set “The letters of the word Mississipi”
- List out the elements of the set “Months of the year”
- Write a verbal description of the set {[latex]3,6,9[/latex]}
- Write a verbal description of the set {a,i,e,o,u}
- Is {[latex]1,3,5[/latex]} a subset of the set of odd integers?
- Is {A,B,C} a subset of the set of letters of the alphabet?
For problems [latex]7-12[/latex], consider the sets below, and indicate if each statement is true or false.
- [latex]3[/latex]∈B
- [latex]5[/latex]∈C
- B⊂A
- C⊂A
- C⊂B
- C⊂U
Using the sets from above, and treating U as the Universal set, find each of the following:
- Using the sets from above, and treating U as the Universal set, find each of the following:
- A∪B
- A∪C
- A∩C
- B∩C
- Ac
- Bc
Let [latex]D={b,a,c,k}[/latex], [latex]E={t,a,s,k}[/latex], [latex]F={b,a,t,h}[/latex]. Using these sets, find the following:
- Dc∩E
- Fc∩D
- (D∩E)∪F
- D∩(E∪P)
- (F∩E)c∩D
- (D∪E)c∩F
Create a Venn diagram to illustrate each of the following:
- (F∩E)∪D
- (D∪E)c∩F
- (Fc∩E′)∩D
- (D∪E)∪Fw
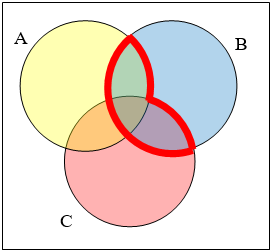
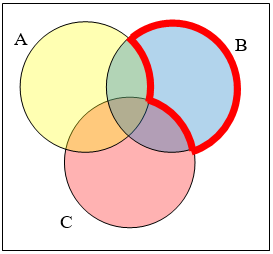
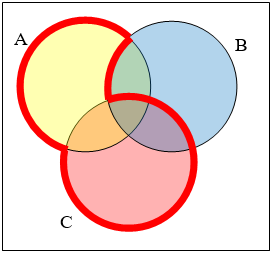
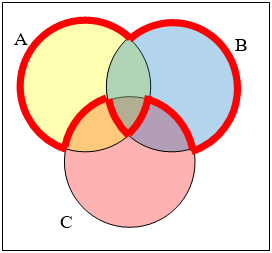
Write an expression for the shaded region.
Let A = {[latex]1,2,3,4,5[/latex]} B = {[latex]1,3,5[/latex]} C = {[latex]4,6[/latex]}. Find the cardinality of the given set.
- n(A)
- n(B)
- n(A∪C)
- n(A∩C)
The Venn diagram here shows the cardinality of each set. Use this in [latex]37-40[/latex] to find the cardinality of given set.
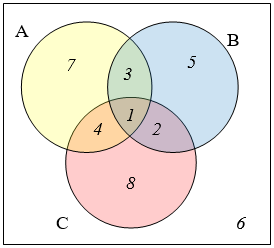
- n(A∩C)
- n(B∪C)
- n(A∩B∩C2)
- n(A∩Bc∩C)
- If n(G) = [latex]20[/latex],n(H) = [latex]30[/latex],n(G ∩ H) = [latex]5[/latex], find n(G ∪ H)
- If n(G) = [latex]5[/latex],n(H) = [latex]8[/latex],n(G ∩ H) = [latex]4[/latex], find n(G ∪ H)
- A survey was given asking whether they watch movies at home from Netflix, Redbox, or a video store. Use the results to determine how many people use Redbox.
[latex]52[/latex] only use Netflix
[latex]62[/latex] only use Redbox
[latex]24[/latex] only use a video store
[latex]16[/latex] use only a video store and Redbox
[latex]48[/latex] use only Netflix and Redbox
[latex]30[/latex] use only a video store and Netflix
[latex]10[/latex] use all three
[latex]25[/latex] use none of these
- A survey asked buyers whether color, size, or brand influenced their choice of cell phone. The results are below. How many people were influenced by brand?
[latex]5[/latex] only said color
[latex]8[/latex] only said size
[latex]16[/latex] only said brand
[latex]20[/latex] said only color and size
[latex]42[/latex] said only color and brand
[latex]53[/latex] said only size and brand
[latex]102[/latex] said all three
[latex]20[/latex] said none of these
- Use the given information to complete a Venn diagram, then determine: a) how many students have seen exactly one of these movies, and b) how many had seen only Star Wars.
[latex]18[/latex] had seen The Matrix (M)
[latex]24[/latex] had seen Star Wars (SW)
[latex]20[/latex] had seen Lord of the Rings (LotR)
[latex]10[/latex] had seen M and SW
[latex]14[/latex] had seen LotR and SW
[latex]12[/latex] had seen M and LotR
[latex]6[/latex] had seen all three
- A survey asked people what alternative transportation modes they use. Using the data to complete a Venn diagram, then determine: a) what percent of people only ride the bus, and b) how many people don’t use any alternate transportation.
[latex]30\%[/latex] use the bus
[latex]20\%[/latex] ride a bicycle
[latex]25\%[/latex] walk
[latex]5\%[/latex] use the bus and ride a bicycle
[latex]10\%[/latex] ride a bicycle and walk
[latex]12\%[/latex] use the bus and walk
[latex]2\%[/latex] use all three
Logic
For questions [latex]47-48[/latex], list the set of integers that satisfy the given conditions.
- A positive multiple of [latex]5[/latex] and not a multiple of [latex]2[/latex]
- Greater than [latex]12[/latex] and less than or equal to [latex]18[/latex]
For questions [latex]49-50[/latex], write the negation of each quantified statement.
- Everyone failed the quiz today.
- Someone in the car needs to use the restroom.
- Translate each statement from symbolic notation into English sentences. Let A represent “Elvis is alive” and let G represent “Elvis gained weight”.
- A∨G
- ∼(A∧G)
- G→∼A
- A↔∼G
For questions [latex]52-55[/latex], create a truth table for each statement.
- A∧∼B
- ∼(∼A∨B)
- A∧B)→C
- A∨B)→∼C
Questions [latex]56-59[/latex]:
In this lesson, we have been studying the inclusive or, which allows both A and B to be true. The exclusive or does not allow both to be true; it translates to “either A or B, but not both.”
- For each situation, decide whether the “or” is most likely exclusive or inclusive.
- An entrée at a restaurant includes soup or a salad.
- You should bring an umbrella or a raincoat with you.
- We can keep driving on I-[latex]5[/latex] or get on I-[latex]405[/latex] at the next exit.
- You should save this document on your computer or a flash drive.
- Complete the truth table for the exclusive or.
- Complete the truth table for (A∨B)∧∼(A∧B)
- Compare your answers for questions 56 and 57. Can you explain the similarities?
- Consider the statement “If you are under age [latex]17[/latex], then you cannot attend this movie.”
- Write the converse.
- Write the inverse.
- Write the contrapositive.
- Assume that the statement “If you swear, then you will get your mouth washed out with soap” is true. Which of the following statements must also be true?
- If you don’t swear, then you won’t get your mouth washed out with soap.
- If you don’t get your mouth washed out with soap, then you didn’t swear.
- If you get your mouth washed out with soap, then you swore.
For questions [latex]62-64[/latex], write the negation of each conditional statement.
- If you don’t look both ways before crossing the street, then you will get hit by a car.
- If Luke faces Vader, then Obi-Wan cannot interfere.
- If you weren’t talking, then you wouldn’t have missed the instructions.
- Assume that the biconditional statement “You will play in the game if and only if you attend all practices this week” is true. Which of the following situations could happen?
- You attended all practices this week and didn’t play in the game.
- You didn’t attend all practices this week and played in the game.
- You didn’t attend all practices this week and didn’t play in the game.
For questions [latex]66-67[/latex], use De Morgan’s Laws to rewrite each conjunction as a disjunction, or each disjunction as a conjunction.
- It is not true that Tina likes Sprite or [latex]7[/latex]-Up.
- It is not the case that you need a dated receipt and your credit card to return this item.
For questions [latex]68-73[/latex], use a Venn diagram or truth table or common form of an argument to decide whether each argument is valid or invalid.
- If a person is on this reality show, they must be self-absorbed. Laura is not self-absorbed. Therefore, Laura cannot be on this reality show.
- If you are a triathlete, then you have outstanding endurance. LeBron James is not a triathlete. Therefore, LeBron does not have outstanding endurance.
- Jamie must scrub the toilets or hose down the garbage cans. Jamie refuses to scrub the toilets. Therefore, Jamie will hose down the garbage cans.
- Some of these kids are rude. Jimmy is one of these kids. Therefore, Jimmy is rude!
- Every student brought a pencil or a pen. Marcie brought a pencil. Therefore, Marcie did not bring a pen.
- If a creature is a chimpanzee, then it is a primate. If a creature is a primate, then it is a mammal. Bobo is a mammal. Therefore, Bobo is a chimpanzee.
For questions [latex]74-76[/latex], name the type of logical fallacy being used.
- If you don’t want to drive from Boston to New York, then you will have to take the train.
- New England Patriots quarterback Tom Brady likes his footballs slightly underinflated. The “Cheatriots” have a history of bending or breaking the rules, so Brady must have told the equipment manager to make sure that the footballs were underinflated.
- Whenever our smoke detector beeps, my kids eat cereal for dinner. The loud beeping sound must make them want to eat cereal for some reason.