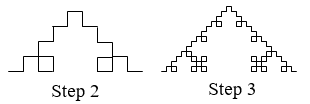
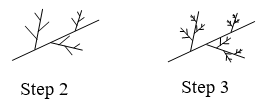
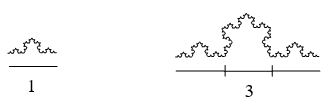
- Four copies of the Koch curve are needed to create a curve scaled by [latex]3[/latex]
[latex]𝐷=log(4)/log(3)≈1.262[/latex]
-
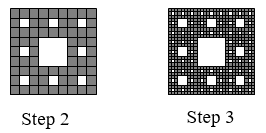
Eight copies of the shape are needed to make a copy scaled by [latex]3[/latex]. [latex]D=\frac{\log (8)}{\log (3)} \approx 1.893[/latex]
-
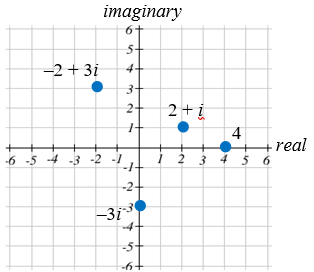
- [latex]5-i[/latex]
- [latex]5-4i[/latex]
-
- [latex]3-5i[/latex]
- [latex]-(6+i)[/latex]
-
- [latex]6+12i[/latex]
- [latex]10-2i[/latex]
- [latex]14+2i[/latex]
-
- [latex]-2+6i[/latex]
- [latex]18+6i[/latex]
- [latex]7+3i[/latex]
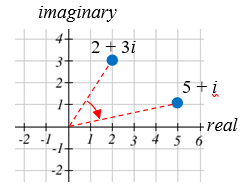
- [latex](2+3i)(1-i) = 5+i.[/latex]It appears that multiplying by [latex]1-i[/latex] both scaled the number away from the origin, and rotated it clockwise about [latex]45°[/latex].
- [latex]z_{1}=i z_{0}+1=i(2)+1=1+2 i[/latex]
[latex]z_{2}=i z_{1}+1=i(1+2 i)+1=i-2+1=-1+i[/latex]
[latex]z_{3}=i z_{2}+1=i(-1+i)+1=-i-1+1=-i[/latex] - [latex]z_{0}=0[/latex]
[latex]z_{1}=z_{0}^{2}-0.25=0-0.25=-0.25[/latex]
[latex]z_{2}=z_{1}^{2}-0.25=(-0.25)^{2}-0.25=-0.1875[/latex]
[latex]z_{3}=z_{2}^{2}-0.25=(-0.1875)^{2}-0.25=-0.21484[/latex]
[latex]z_{4}=z_{3}^{2}-0.25=(-0.21484)^{2}-0.25=-0.20384[/latex] - attracted, to approximately [latex]-0.3776+0.14242i[/latex]
- periodic [latex]2[/latex]-cycle
- Escaping
- periodic [latex]3[/latex]-cycle