Historical Counting Systems: Get Stronger Answer Key

  1. Partial answer: Jars: [latex]3[/latex] singles, [latex]3[/latex] @ [latex]x3, 2[/latex] @ [latex]x6,1[/latex]@ [latex]x12.3[/latex] + [latex]9[/latex] + [latex]12[/latex] + [latex]12[/latex] = [latex]36[/latex]
  3. [latex]113[/latex]
  5. [latex]3022[/latex]
  7. [latex]53[/latex]
  9. [latex]1100100[/latex]
  11. [latex]332[/latex]
  13. [latex]111100010[/latex]
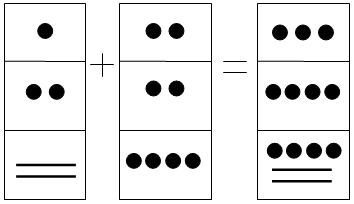
  15. [latex]135[/latex] = [latex]6,15[/latex] base [latex]20[/latex] = 2 compartments with Mayan symbols - from the bottom: three horizontal lines and one horizontal line and one dot stacked
  17. [latex]360[/latex] = [latex]18, 0[/latex] base [latex]20[/latex] = Two compartments with Mayan symbols - from the bottom: one shell, and three lines with three dots stacked
  19. [latex]10500[/latex] = [latex]1,6,5,0[/latex] base [latex]20[/latex] Four compartments with Mayan symbols - from the bottom, one shell, one horizontal line, one horizontal line with one dot stacked, and one dot
  21. [latex]1,2,12[/latex] base [latex]20[/latex] = [latex]452[/latex] base [latex]10[/latex]
  23. [latex]3,0,3[/latex] base [latex]20[/latex] = [latex]1203[/latex] base [latex]10[/latex]
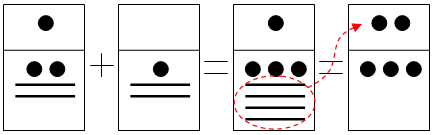
  25. [latex]32+11=1,12_{20}+11_{20}=1,23_{20}=2,3_{20}=43[/latex]
    An equation done with Mayan symbols. Two compartments of two lines with two dots stacked in the first and one dot in the second is added to a compartment with two lines and a dot. This is shown to equal two compartments with four lines and three dots stacked on top in the first compartment and one dot in the second compartment. This is shown to also be equal to two compartments with three dots in the first compartment and two dots in the second compartment. The four lines from the other side of the equation have been circled and there is an arrow pointing at one of the dots in the top compartment with two dots.
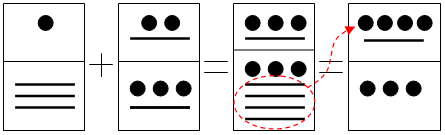
  27. [latex]35+148=1,15_{20}+7,8_{20}=8,23_{20}=9,320=183[/latex]
    An equation done with Mayan symbols. Two compartments of three lines in the first and one dot in the second is added to two compartments with one line and three dots stacked on top in the first and one line and two dots stacked on top in the second one. This is shown to equal two compartments with four lines and three dots stacked on top in the first compartment and one line with three dots stacked on top in the second compartment. This is shown to also be equal to two compartments with three dots in the first compartment and one line with four dots stacked in the second compartment. The four lines from the other side of the equation have been circled and there is an arrow pointing at one of the dots in the top compartment with the one line and four dots stacked.
  29. [latex]450+844=1,2,10_{20}+2,2,4_{20}=3,4,14_{20}=1294[/latex]
    An equation done with Mayan symbols. One set of three compartments is added to another set of three to equal another set of three. From bottom to top, the first set consists of two horizontal lines, two dots, and one dot and the second set consists of four dots, two dots, and two dots. On the other side of the equation, from bottom to top, the compartments consist of two lines with four dots stacked, four dots, and three dots.