Whole Numbers: Fresh Take

  • Identify whole numbers and counting numbers
  • Write whole numbers in words
  • Round whole numbers
  • Add, subtract, multiply, and divide whole numbers

Whole Numbers and Place Value

The Main Idea 

Counting numbers start with [latex]1[/latex] and continue.

Whole numbers are the counting numbers and zero.

Finding the place value of a whole number primarily revolves around recognizing the value each digit holds based on its position in the number. Starting from the right, the first digit represents ones, followed by tens, hundreds, thousands, and so on as we move leftwards.

Which of the following are

  1. counting numbers?
  2. whole numbers?

[latex]0,\frac{1}{4},3,5.2,15,105[/latex]

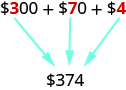
Money gives us another, more familiar model of place value. Suppose a wallet contains three [latex]$100[/latex] bills, seven [latex]$10[/latex] bills, and four [latex]$1[/latex] bills. The amounts are summarized in the image below. How much money is in the wallet?

Three groups of dollar bills. The first group is labeled 'Three $100 bills. 3 times $100 = $300,' the second is labeled 'Seven $10 bills. 7 times $10 = $70,' and the third is labeled 'Four $1 bills. 4 times $1 = $4.'

 

Find the total value of each kind of bill, and then add to find the total. The wallet contains [latex]$374[/latex].

$300 + $70 + $4 adding up to $374.

 

You can view the transcript for “Finding the Value of the Underlined Digit | Whole Number Place Value | Math with Mr. J” here (opens in new window).

The video below shows more examples of how to determine the place value of a digit in a number.

You can view the transcript for “Examples: Determining Place Value” here (opens in new window).

Use Place Value to Write Whole Numbers

The Main Idea

Name a whole number in words

  1. Starting at the digit on the left, name the number in each period, followed by the period name. Do not include the period name for the ones.
  2. Use commas in the number to separate the periods.

Write a whole number from words

  1. Identify the words that indicate periods. (Remember the ones period is never named).
  2. Draw three blanks to indicate the number of places needed in each period. Separate the periods by commas.
  3. Name the number in each period and place the digits in the correct place value position.
A state budget was about [latex]\text{\$77}[/latex] billion. Write the budget in standard form.

 

Write each number in standard form:

  1. The closest distance from Earth to Mars is about [latex]34[/latex] million miles.
  2. The total weight of an aircraft carrier is [latex]204[/latex] million pounds.

The video below shows more examples of how to use place value to write the name of a whole number.

You can view the transcript for “Example: Write a Whole Number in Digits from Words” here (opens in new window).

Rounding Whole Numbers

The Main Idea 

Rounding is a method used to shorten or simplify numbers by adjusting them to the closest specified value.

To round a whole number to a specific place value:

  1. Locate the given place value. All digits to the left of that place value do not change.
  2. Underline the digit to the right of the given place value.
  3. Determine if this digit is greater than or equal to [latex]5[/latex].
    • Yes—add [latex]1[/latex] to the digit in the given place value.
    • No—do not change the digit in the given place value.
  4. Replace all digits to the right of the given place value with zeros.
If the digit to the right of your given place value is [latex]5[/latex] or above, give your given place value a shove. If the digit to the right of your given place value is [latex]4[/latex] or less, let your given place value rest.

Watch the video below for more examples of how to round whole numbers to a given place value.

You can view the transcript for “Ex: Rounding to the Various Place Values – Number Line / Formal Rules” here (opens in new window).

Addition of Whole Numbers

The Main Idea 

Addition of whole numbers involves combining the values of two or more numbers, using the plus (+) sign as the notation.

Operation Notation Expression Read as Result
Addition [latex]+[/latex] [latex]3+4[/latex] three plus four the sum of [latex]3[/latex] and [latex]4[/latex]

 

The identity property of addition states that when a number is added to zero, the original number remains unchanged. This underscores the fact that zero is the ‘identity’ for addition.

The commutative property of addition, on the other hand, affirms that the order in which numbers are added does not affect the result, that is, for any two whole numbers [latex]a[/latex] and [latex]b[/latex], [latex]a + b[/latex] equals [latex]b + a[/latex].

Addition is really just counting. This is easy to see by modeling. We will model addition with base-[latex]10[/latex] blocks. Remember, a block represents [latex]1[/latex] and a rod represents [latex]10[/latex]. Let’s start by modeling the addition expression we just considered, [latex]3+4[/latex].
Each addend is less than [latex]10[/latex], so we can use ones blocks.

We start by modeling the first number with [latex]3[/latex] blocks. Three individual blocks
Then we model the second number with [latex]4[/latex] blocks. Three individual blocks next to four individual blocks
Count the total number of blocks. 7 individual blocks

 

There are [latex]7[/latex] blocks in all. We use an equal sign [latex]\text{(=)}[/latex] to show the sum. A math sentence that shows that two expressions are equal is called an equation. We have shown that. [latex]3+4=7[/latex].

Model the addition [latex]2+6[/latex].

When the result is [latex]10[/latex] or more ones blocks, we will exchange the [latex]10[/latex] blocks for one rod.

Next we will model adding two digit numbers.

Model each addition:

  1. [latex]15+27[/latex]
  2. [latex]16+29[/latex]

Watch the video below for another example of how to use base [latex]10[/latex] blocks to model the sum of two whole numbers.

You can view the transcript for “Model Addition of Two Digit Whole Numbers Using Base Ten Blocks” here (opens in new window).

Subtraction of Whole Numbers

The Main Idea 

Subtraction of whole numbers is the process of taking away one number from another to find the difference, often represented with a minus (-) sign.

Operation Notation Expression Read as Result
Subtraction [latex]-[/latex] [latex]7 - 3[/latex] seven minus three the difference of [latex]7[/latex] and [latex]3[/latex]

A model can help us visualize the process of subtraction much as it did with addition. Again, we will use [latex]\text{base - 10}[/latex] blocks. Remember a block represents [latex]1[/latex] and a rod represents [latex]10[/latex]. Let’s start by modeling the subtraction expression we just considered, [latex]7 - 3[/latex].

We start by modeling the first number, [latex]7[/latex]. 7 individual blocks
Now take away the second number, [latex]3[/latex]. We’ll circle [latex]3[/latex] blocks to show that we are taking them away. 3 individual blocks in a circle and 4 individual blocks outside of it
Count the number of blocks remaining. 4 individual blocks
There are [latex]4[/latex] ones blocks left. We have shown that [latex]7 - 3=4[/latex] .
Model the subtraction: [latex]8 - 2[/latex]

As we did with addition, we can describe the models as ones blocks and tens rods, or we can simply say ones and tens. Next we will model subtracting two digit numbers.

Model each subtraction:

  1. [latex]42 - 27[/latex]
  2. [latex]45 - 29[/latex]

Watch the video below to see more examples of using base 10 blocks to model subtraction.

You can view the transcript for “Model Subtraction of Two Digit Whole Numbers Using Base Ten Blocks” here (opens in new window).

Watch the video below to see another example of subtracting whole numbers by lining up place values.

You can view the transcript for “Example: Subtracting Whole Numbers” here (opens in new window).

Multiplying Whole Numbers

The Main Idea 

Multiplication of whole numbers is a process where one number, known as a factor, is repeatedly added to itself based on the value of the second factor, resulting in a total called the product.

Operation Notation Expression Read as Result
[latex]\text{Multiplication}[/latex] [latex]\times[/latex]
[latex]\cdot[/latex]
[latex]\left(\right)[/latex] 		[latex]3\times 8[/latex]
[latex]3\cdot 8[/latex]
[latex]3\left(8\right)[/latex] 		[latex]\text{three times eight}[/latex] [latex]\text{the product of 3 and 8}[/latex]

 

The multiplication property of zero states the product of any number and [latex]0[/latex] is [latex]0[/latex].

The identity property of multiplication states the product of any number and [latex]1[/latex] is the number.

The commutative property of multiplication states that changing the order of the factors does not change their product.

Just like with subtraction and addition, modeling multiplication can help with understanding what is going on. There are many ways to model multiplication. Unlike in the previous sections where we used base-[latex]10[/latex] blocks, here we will use counters to help us understand the meaning of multiplication. A counter is any object that can be used for counting. We will use round blue counters. Let’s start by modeling the multiplication expression we just considered, [latex]3\times 8[/latex].

To model the product [latex]3\times 8[/latex], we’ll start with a row of [latex]8[/latex] counters.

An image of a horizontal row of 8 counters.

 

The other factor is [latex]3[/latex], so we’ll make [latex]3[/latex] rows of [latex]8[/latex] counters.

An image of 3 horizontal rows of counters, each row containing 8 counters.

 

Now we can count the result. There are [latex]24[/latex] counters in all.

[latex]3\times 8=24[/latex]

 

If you look at the counters sideways, you’ll see that we could have also made [latex]8[/latex] rows of [latex]3[/latex] counters.

Model each multiplication:

  1. [latex]4\times 6[/latex]
  2. [latex]5\times 7[/latex]

In the video below, we summarize the concepts covered in multiplying whole numbers including the multiplication property of zero, the identity property of multiplication, and the commutative property of multiplication.

You can view the transcript for “Multiplying Whole Numbers” here (opens in new window).

Dividing Whole Numbers

The Main Idea 

Division of whole numbers involves partitioning a given quantity, known as the dividend, into equal parts, with the number of these parts represented by the divisor, resulting in the quotient.

Operation Notation Expression Read as Result
[latex]\text{Division}[/latex] [latex]a \div b[/latex]
[latex]\frac{a}{b}[/latex]
[latex]b\overline{)a}[/latex]
[latex]a/b[/latex] 		[latex]12\div 4[/latex]
[latex]\frac{12}{4}[/latex]
[latex]4\overline{)12}[/latex]
[latex]12/4[/latex] 		[latex]\text{Twelve divided by four}[/latex] [latex]\text{the quotient of 12 and 4}[/latex]

 

The division properties of one states dividing any number, except [latex]0[/latex], by itself produces a quotient of [latex]1[/latex] and any number divided by [latex]1[/latex] produces a quotient of the number.

The division properties of zero states any number divided by zero is undefined, while zero divided by any number (except zero) is always zero.

As we did with multiplication, we will model division using counters. The operation of division helps us organize items into equal groups as we start with the number of items in the dividend and subtract the number in the divisor repeatedly. Let’s start by modeling the division expression we just considered, [latex]24\div 8[/latex].

To find the quotient [latex]24\div 8[/latex], we want to know how many groups of [latex]8[/latex] are in [latex]24[/latex].
Model the dividend. Start with [latex]24[/latex] counters.

An image of 24 counters placed randomly.

 

The divisor tell us the number of counters we want in each group. Form groups of [latex]8[/latex] counters.

An image of 24 counters, all contained in 3 bubbles, each bubble containing 8 counters.

 

Count the number of groups. There are [latex]3[/latex] groups.

[latex]24\div 8=3[/latex]

 

Model each division:

  1. [latex]24\div 6[/latex]
  2. [latex]42\div 7[/latex]

In the video below we show another way to model division using area.

You can view the transcript for “Division of Whole Numbers using Area (No Remainder)” here (opens in new window).

In the video below we show another example of using long division.

You can view the transcript for “Ex: Long Division – Two Digit Divided by One Digit (No Remainder)” here (opens in new window).

Watch this video for another example of how to use long division to divide a four digit whole number by a two digit whole number.

You can view the transcript for “Example: Dividing Whole Numbers without a Remainder” here (opens in new window).

Watch the video below for another example of how to use long division to divide whole numbers when there is a remainder.

You can view the transcript for “Example: Dividing Whole Numbers with a Remainder” here (opens in new window).

For a review of adding, subtracting, multiplying, and division of whole numbers watch the following video.

You can view the transcript for “Whole Number Operations | Adding, Subtracting, Multiplying, and Dividing” here (opens in new window).