- Understand different number systems
- Convert different number systems
and so on.
In our base-[latex]10[/latex] system, a number like [latex]5,783,216[/latex] has meaning to us because we are familiar with the system and its places. As we know, there are six ones, since there is a [latex]6[/latex] in the ones place. Likewise, there are seven “hundred thousands,” since the [latex]7[/latex] resides in that place. Each digit has a value that is explicitly determined by its position within the number. We make a distinction between digit, which is just a symbol such as [latex]5[/latex], and a number, which is made up of one or more digits. We can take this number and assign each of its digits a value. One way to do this is with a table, which follows:
| [latex]5,000,000[/latex] | [latex]= 5 × 1,000,000[/latex] | [latex]= 5 × 10^6[/latex] | [latex]\text{Five million}[/latex] | ||||
| [latex]+700,000[/latex] | [latex]=7 × 100,000[/latex] | [latex]=7 × 10^5[/latex] | [latex]\begin{align}\text{Seven hundred} \text{ thousand}\end{align}[/latex] | ||||
| [latex]+80,000[/latex] | [latex]= 8 × 10,000[/latex] | [latex]= 8 × 10^4[/latex] | [latex]\text{Eighty thousand}[/latex] | ||||
| [latex]+3,000[/latex] | [latex]= 3 × 1000[/latex] | [latex]= 3 × 10^3[/latex] | [latex]\text{Three thousand}[/latex] | ||||
| [latex]+200[/latex] | [latex]= 2 × 100[/latex] | [latex]= 2 × 10^2[/latex] | [latex]\text{Two hundred}[/latex] | ||||
| [latex]+10[/latex] | [latex]= 1 × 10[/latex] | [latex]= 1 × 10^1[/latex] | [latex]\text{Ten}[/latex] | ||||
| [latex]+6[/latex] | [latex]= 6 × 1[/latex] | [latex]= 6 × 10^0[/latex] | [latex]\text{Six}[/latex] | ||||
| [latex]5,783,216[/latex] | [latex][/latex] | [latex][/latex] | [latex]\begin{align} \hspace{0.8cm} \text{Five million, seven hundred} \\ \hspace{0.8cm} \text{eighty-three thousand, two hundred sixteen}\end{align}[/latex] | ||||
From the third column in the table, we can see that each place is simply a multiple of ten. Of course, this makes sense given that our base is ten. The digits that are multiplying each place simply tell us how many of that place we have. We are restricted to having at most [latex]9[/latex] in any one place before we have to “carry” over to the next place. We cannot, for example, have [latex]11[/latex] in the hundreds place. Instead, we would carry [latex]1[/latex] to the thousands place and retain [latex]1[/latex] in the hundreds place. This comes as no surprise to us since we readily see that [latex]11[/latex] hundreds is the same as one thousand, one hundred. Carrying is a pretty typical occurrence in a base system.
Watch this video to see more examples of converting numbers in bases other than [latex]10[/latex] into a base-[latex]10[/latex] number.
You can view the transcript for “Convert Numbers in Base Ten to Different Bases: Remainder Method” here (opens in new window).
Another Method For Converting From Base-[latex]10[/latex] to Other Bases
As budding mathematicians, you should always be asking questions like “How could I simplify this process?” In general, that is one of the main things that mathematicians do: they look for ways to take complicated situations and make them easier or more familiar. In this section we will attempt to do that. To do so, we will start by looking at our own decimal system. What we do may seem obvious and maybe even intuitive but that’s the point. We want to find a process that we readily recognize works and makes sense to us in a familiar system and then use it to extend our results to a different, unfamiliar system.
Let’s start with the decimal number, [latex]4863_{10}[/latex]. We will convert this number to base-[latex]10[/latex]. Yeah, I know it’s already in base-[latex]10[/latex], but if you carefully follow what we’re doing, you’ll see it makes things work out very nicely with other bases later on. We first note that the highest power of [latex]10[/latex] that will divide into [latex]4863[/latex] at least once is [latex]10^3 = 1000[/latex]. In general, this is the first step in our new process; we find the highest power of a given base that will divide at least once into our given number.
We now divide [latex]1000[/latex] into [latex]4863[/latex]:
[latex]4863 ÷ 1000 = 4.863[/latex]
This says that there are four thousands in [latex]4863[/latex] (obviously). However, it also says that there are [latex]0.863[/latex] thousands in [latex]4863[/latex]. This fractional part is our remainder and will be converted to lower powers of our base ([latex]10[/latex]). If we take that decimal and multiply by [latex]10[/latex] (since that’s the base we’re in) we get the following:
[latex]0.863 × 10 = 8.63[/latex]
Why multiply by [latex]10[/latex] at this point? We need to recognize here that [latex]0.863[/latex] thousands is the same as [latex]8.63[/latex] hundreds. Think about that until it sinks in.
[latex](0.863)(1000) = 863[/latex]
[latex](8.63)(100) = 863[/latex]
These two statements are equivalent. So, what we are really doing here by multiplying by [latex]10[/latex] is rephrasing or converting from one place (thousands) to the next place down (hundreds).
[latex]0.863 × 10 \Rightarrow 8.63[/latex]
[latex](\text{Parts of Thousands}) × 10 \Rightarrow \text{Hundreds}[/latex]
What we have now is [latex]8[/latex] hundreds and a remainder of [latex]0.63[/latex] hundreds, which is the same as [latex]6.3[/latex] tens. We can do this again with the [latex]0.63[/latex] that remains after this first step.
[latex]0.63 × 10 \Rightarrow 6.3[/latex]
[latex]\text{Hundreds} × 10 \Rightarrow \text{Tens}[/latex]
So we have six tens and [latex]0.3[/latex] tens, which is the same as [latex]3[/latex] ones, our last place value.
Now here’s the punch line. Let’s put all of the together in one place:
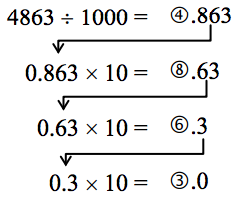
Note that in each step, the remainder is carried down to the next step and multiplied by [latex]10[/latex], the base. Also, at each step, the whole number part, which is circled, gives the digit that belongs in that particular place. What is amazing is that this works for any base! So, to convert from a base-[latex]10[/latex] number to some other base, [latex]b[/latex], we have the following steps we can follow:
How to: Convert from Base-[latex]10[/latex] to Base-[latex]b[/latex]: Another method
- Find the highest power of the base-[latex]b[/latex] that will divide into the given number at least once and then divide.
- Keep the whole number part, and multiply the fractional part by the base-[latex]b[/latex].
- Repeat step two, keeping the whole number part (including [latex]0[/latex]), carrying the fractional part to the next step until only a whole number result is obtained.
- Collect all your whole number parts to get your number in base-[latex]b[/latex] notation.
We will illustrate this procedure with some examples.
We can compare our result with what we saw earlier, or simply check with our calculator, and find that these two numbers really are equivalent to each other.
This last example shows the importance of using a calculator in certain situations and taking care to avoid clearing the calculator’s memory or display until you get to the very end of the process.
If we round, even to two decimal places in each step, clearing our calculator out at each step along the way, we will get a series of numbers that do not terminate but begin repeating themselves endlessly. (Try it!) We end up with something that doesn’t make any sense, at least not in this context. So be careful to use your calculator cautiously on these conversion problems.
Also, remember that if your first division is by [latex]7^{5}[/latex], then you expect to have [latex]6[/latex] digits in the final answer, corresponding to the places for [latex]7^{5}[/latex], [latex]7^{4}[/latex], and so on down to [latex]7^{0}[/latex]. If you find yourself with more than [latex]6[/latex] digits due to rounding errors, you know something went wrong.
The following video shows how to use a calculator to convert numbers in base-[latex]10[/latex] into other bases.
You can view the transcript for “Convert Numbers in Base Ten to Different Bases: Calculator Method” here (opens in new window).
