Math in Arts: Background You’ll Need 1

  • Identify how functions slide

Vertical Shift

One kind of transformation involves shifting the entire graph of a function up, down, right, or left. The simplest shift is a vertical shift, moving the graph up or down, because this transformation involves adding a positive or negative constant to the function. In other words, we add the same constant to the output value of the function regardless of the input. For a function [latex]g\left(x\right)=f\left(x\right)+k[/latex], the function [latex]f\left(x\right)[/latex] is shifted vertically [latex]k[/latex] units.

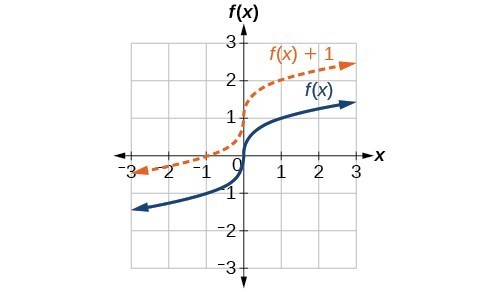
Graph of f of x equals the cubed root of x shifted upward one unit, the resulting graph passes through the point (0,1) instead of (0,0), (1, 2) instead of (1,1) and (-1, 0) instead of (-1, -1)
Vertical shift by [latex]k=1[/latex] of the cube root function [latex]f\left(x\right)=\sqrt[3]{x}[/latex].

 

To help you visualize the concept of a vertical shift, consider that [latex]y=f\left(x\right)[/latex]. Therefore, [latex]f\left(x\right)+k[/latex] is equivalent to [latex]y+k[/latex]. Every unit of [latex]y[/latex] is replaced by [latex]y+k[/latex], so the [latex]y\text{-}[/latex] value increases or decreases depending on the value of [latex]k[/latex]. The result is a shift upward or downward.

vertical shift

Given a function [latex]f\left(x\right)[/latex], a new function [latex]g\left(x\right)=f\left(x\right)+k[/latex], where [latex]k[/latex] is a constant, is a vertical shift of the function [latex]f\left(x\right)[/latex]. All the output values change by [latex]k[/latex] units. If [latex]k[/latex] is positive, the graph will shift up. If [latex]k[/latex] is negative, the graph will shift down.

Horizontal Shift

We just saw that the vertical shift is a change to the output, or outside, of the function. We will now look at how changes to input, on the inside of the function, change its graph and meaning. A shift to the input results in a movement of the graph of the function left or right in what is known as a horizontal shift.

Graph of f of x equals the cubed root of x shifted left one unit, the resulting graph passes through the point (0,-1) instead of (0,0), (0, 1) instead of (1,1) and (-2, -1) instead of (-1, -1)
Horizontal shift of the function [latex]f\left(x\right)=\sqrt[3]{x}[/latex]. Note that [latex]h=+1[/latex] shifts
the graph to the left, that is, towards negative values of [latex]x[/latex].

 

For example, if [latex]f\left(x\right)={x}^{2}[/latex], then [latex]g\left(x\right)={\left(x - 2\right)}^{2}[/latex] is a new function. Each input is reduced by 2 prior to squaring the function. The result is that the graph is shifted 2 units to the right, because we would need to increase the prior input by 2 units to yield the same output value as given in [latex]f[/latex].

horizontal shift

Given a function [latex]f[/latex], a new function [latex]g\left(x\right)=f\left(x-h\right)[/latex], where [latex]h[/latex] is a constant, is a horizontal shift of the function [latex]f[/latex]. If [latex]h[/latex] is positive, the graph will shift right. If [latex]h[/latex] is negative, the graph will shift left.