General Problem Solving: Background You’ll Need 3

  • Multiply and Divide Fractions

Multiply Fractions

There are many times when it is necessary to multiply fractions. A model may help you understand multiplication of fractions.

When you multiply a fraction by a fraction, you are finding a “fraction of a fraction.” Suppose you have [latex]\frac{3}{4}[/latex] of a candy bar and you want to find [latex]\frac{1}{2}[/latex] of the [latex]\frac{3}{4}[/latex]:

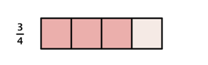
3 out of four boxes are shaded. This is 3/4.

 

By dividing each fourth in half, you can divide the candy bar into eighths.

Six of 8 boxes are shaded. This is 6/8.

 

Then, choose half of those to get [latex]\frac{3}{8}[/latex].

Six of 8 boxes are shaded, and of those six, three of them are shaded purple. The 3 purple boxes represent 3/8.

 

In the above case, to find the answer, you can multiply the numerators together and the denominators together.

Multiplying Two Fractions

Multiplying two fractions is a fundamental arithmetic operation where each numerator is multiplied by the other fraction’s numerator and each denominator by the other’s denominator, resulting in a new fraction that represents the product of the two original fractions.

 

[latex]\frac{a}{b}\cdot \frac{c}{d}=\frac{a\cdot c}{b\cdot d}=\frac{\text{product of the numerators}}{\text{product of the denominators}}[/latex]

Multiplying More Than Two Fractions

When multiplying more than two fractions, you continue the process of multiplying numerators together and denominators together.

 

[latex]\frac{a}{b}\cdot \frac{c}{d}\cdot \frac{e}{f}=\frac{a\cdot c\cdot e}{b\cdot d\cdot f}[/latex]
  • product: the result of  multiplication
  • factor: something being multiplied – for  [latex]3 \cdot 2 = 6[/latex] , both [latex]3[/latex] and [latex]2[/latex] are factors of [latex]6[/latex]
  • numerator: the top part of a fraction – the numerator in the fraction [latex]\frac{2}{3}[/latex] is [latex]2[/latex]
  • denominator: the bottom part of a fraction – the denominator in the fraction [latex]\frac{2}{3}[/latex] is [latex]3[/latex]
Multiply [latex]\frac{2}{3}\cdot \frac{4}{5}[/latex].

Divide Fractions

Dividing fractions is a key mathematical skill that extends our understanding of division beyond the realm of whole numbers. When we divide by a fraction, we are essentially asking how many of these fractional parts fit into the whole or another fraction. This process involves inverting the divisor (the fraction by which we are dividing) and then multiplying it by the dividend (the fraction to be divided).

Dividing is Multiplying by the Reciprocal

For all division, you can turn the operation into multiplication by using the reciprocal. Dividing is the same as multiplying by the reciprocal.

  • reciprocal: two fractions are reciprocals if their product is [latex]1[/latex] (Don’t worry; we will show you examples of what this means.)
  • quotient: the result of division

How To: Dividing with Fractions

  1. Find the reciprocal of the number that follows the division symbol.
  2. Multiply the first number (the one before the division symbol) by the reciprocal of the second number (the one after the division symbol).

Any easy way to remember how to divide fractions is the phrase “keep, change, flip.” This means to KEEP the first number, CHANGE the division sign to multiplication, and then FLIP (use the reciprocal) of the second number.

Division by Zero

Caution! Division by zero is undefined and so is the reciprocal of any fraction that has a zero in the numerator. For any real number [latex]a[/latex], [latex]\frac{a}{0}[/latex] is undefined.

 

Additionally, the reciprocal of [latex]\frac{0}{a}[/latex] will always be [latex]0[/latex].

Find [latex]\frac{2}{3}\div 4[/latex].

Divide [latex]\frac{2}{3}\div \frac{1}{6}[/latex].