• Understand early counting systems and their representation of numbers
• Recognize the chronological order of counting system development
• Convert Hindu-Arabic and Roman Numerals

Unlocking the Mayan Code: Understanding the Vigesimal System

Step into the world of the ancient Mayan civilization and unravel the mysteries of their unique numerical system.

The Mayan civilization is generally dated from 1500 BCE to 1700 CE. The Yucatan Peninsula (see figure 16^[1]) in Mexico was the scene for the development of one of the most advanced civilizations of the ancient world. The Mayans had a sophisticated ritual system that was overseen by a priestly class. This class of priests developed a philosophy with time as divine and eternal.^[2] The calendar, and calculations related to it, were thus very important to the ritual life of the priestly class, and hence the Mayan people. In fact, much of what we know about this culture comes from their calendar records and astronomy data. Another important source of information on the Mayans is the writings of Father Diego de Landa, who went to Mexico as a missionary in 1549.

There were two numeral systems developed by the Mayans—one for the common people and one for the priests. Not only did these two systems use different symbols, they also used different base systems. For the priests, the number system was governed by ritual. The days of the year were thought to be gods, so the formal symbols for the days were decorated heads,^[3] like the sample to the right^[4] Since the basic calendar was based on 360 days, the priestly numeral system used a mixed base system employing multiples of 20 and 360. This makes for a confusing system, the details of which we will skip.

Instead, we will focus on the numeration system of the “common” people, which used a more consistent base system. The “common” people used a base-20 system called the “vigesimal” system. This system was positional, where the place of a numeric symbol indicates its place value, similar to the decimal system we use today. One of the unique features of this system is the usage of only three symbols to represent all numbers. The Mayans might have been the pioneers in using zero as a placeholder/number.^[5]

 

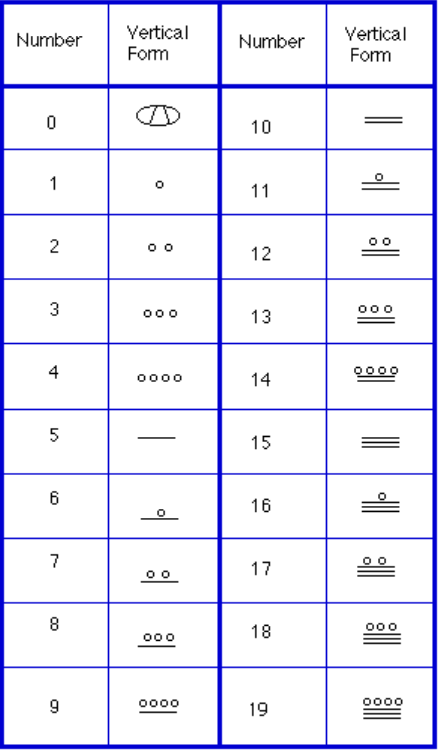
In order to write numbers down, there were only three symbols needed in this system. A horizontal bar represented the quantity [latex]5[/latex], a dot represented the quantity [latex]1[/latex], and a special symbol (thought to be a shell) represented zero. The Mayan system may have been the first to make use of zero as a placeholder/number. The first [latex]20[/latex] numbers are shown in the table to the above.^[6]

Unlike our system, where the ones place starts on the right and then moves to the left, the Mayan systems places the ones on the bottom of a vertical orientation and moves up as the place value increases.

When numbers are written in vertical form, there should never be more than four dots in a single place. When writing Mayan numbers, every group of five dots becomes one bar. Also, there should never be more than three bars in a single place…four bars would be converted to one dot in the next place up. It’s the same as [latex]10[/latex] getting converted to a [latex]1[/latex] in the next place up when we carry during addition.

In this activity, you will learn how to interpret and manipulate the Mayan numerical system. You will be given a series of tasks that will help you understand and analyze this unique system. Ready to unlock the secrets of the Mayan code?

---