- Apply basic probability concepts
Probability
events and outcomes
- The result of an experiment is called an outcome.
- An event is any particular outcome or group of outcomes.
- A simple event is an event that cannot be broken down further.
- A compound event is a combination of two or more simple events.
- The sample space is the set of all possible simple events.
basic probability
Given that all outcomes are equally likely, we can compute the probability of an event [latex]E[/latex] using this formula:
[latex]P(E)=\frac{\text{Number of outcomes corresponding to the event E}}{\text{Total number of equally-likely outcomes}}[/latex]
Probabilities can be expressed as decimals, fractions, or percentages.
Notation: The probability of an event is notated as [latex]P(\text{event})[/latex]
certain and impossible events
- An impossible event has a probability of [latex]0[/latex].
- A certain event has a probability of [latex]1[/latex].
- The probability of any event must be [latex]0\le P(E)\le 1[/latex]
Probability of Two Independent Events
Suppose we flipped a coin and rolled a die, and wanted to know the probability of getting a head on the coin and a [latex]6[/latex] on the die. Take a moment to think about how you could approach finding the probability. You could start by listing all the possible outcomes: [latex]{H1, H2, H3, H4, H5, H6, T1, T2, T3, T4, T5, T6}[/latex] and determining the total number of outcomes. Notice, out of the twelve outcomes only one is the desired outcome, so the probability is [latex]\frac{1}{12}[/latex]. This example contains two independent events since getting a certain outcome from rolling a die had no influence on the outcome from flipping the coin. When two events are independent, the probability of both occurring is the product of the probabilities of the individual events.
independent events
Events [latex]A[/latex] and [latex]B[/latex] are independent events if the probability of event [latex]B[/latex] occurring is the same whether or not event [latex]A[/latex] occurs.
[latex]P(A \text{ and } B)[/latex] for independent events
If events [latex]A[/latex] and [latex]B[/latex] are independent, then the probability of both [latex]A[/latex] and [latex]B[/latex] occurring is:
where [latex]P(A \text{ and } B)[/latex] is the probability of events [latex]A[/latex] and [latex]B[/latex] both occurring, [latex]P(A)[/latex] is the probability of event [latex]A[/latex] occurring, and [latex]P(B)[/latex] is the probability of event [latex]B[/latex] occurring.
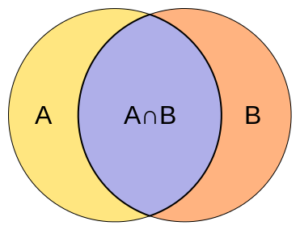
Notation: [latex]P\left(A\text{ and }B\right)[/latex] can also be notated as [latex]P(A \cap B)[/latex]
[latex]P(A \text{ or } B)[/latex] for independent events

The probability of either [latex]A[/latex] or [latex]B[/latex] occurring (or both) is:
[latex]P(A\text{ or }B)=P(A)+P(B)–P(A\text{ and }B)[/latex]
Notation: [latex]P\left(A\text{ or }B\right)[/latex] can also be notated as [latex]P(A \cup B)[/latex]
Conditional Probability
So far we have computed the probabilities of events that were independent of each other. We saw that getting a certain outcome from rolling a die had no influence on the outcome from flipping a coin, even though we were computing a probability based on doing them at the same time. In this section, we will consider events that are dependent on each other, called conditional probabilities.
conditional probability
The probability the event [latex]B[/latex] occurs, given that event [latex]A[/latex] has happened, is represented as:
[latex]P(B | A)[/latex]
This is read as “the probability of [latex]B[/latex] given [latex]A[/latex].”
Conditional Probability Formula:
If Events [latex]A[/latex] and [latex]B[/latex] are not independent, then [latex]P(A \text{ and } B) = P(A) · P(B | A)[/latex]
It’s important to remember the conditional probability formula can also be written as [latex]P(A \text{ and } B) = P(B) · P(A|B)[/latex].