Vertical Angles
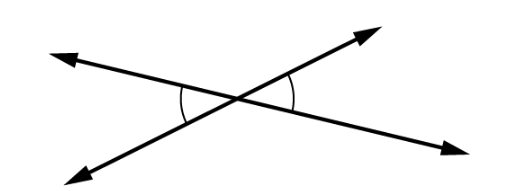
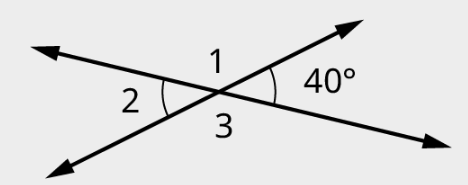
When two lines intersect, the opposite angles are called vertical angles, and vertical angles have equal measure. For example, the image below shows two straight lines intersecting each other. One set of opposite angles shows angle markers; those angles have the same measure. The other two opposite angles have the same measure as well.
vertical angles
Vertical angles are a pair of opposite angles that are formed when two lines intersect. These angles are located across from each other and share a common vertex or point of intersection. Vertical angles have equal measures, which means they have the same angle measurement.
Transversals
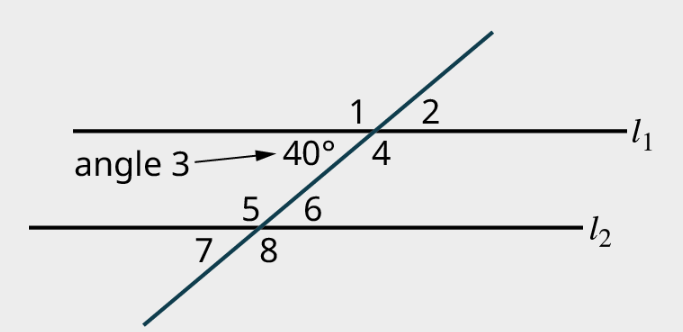
When two parallel lines are crossed by a straight line or transversal, eight angles are formed, including alternate interior angles, alternate exterior angles, corresponding angles, vertical angles, and supplementary angles. In the image below, angles [latex]1[/latex], [latex]2[/latex], [latex]7[/latex], and [latex]8[/latex] are called exterior angles, and angles [latex]3[/latex], [latex]4[/latex], [latex]5[/latex], and [latex]6[/latex] are called interior angles.

Alternate interior angles are the interior angles on opposite sides of the transversal. These two angles have the same measure. For example in the image below, [latex]∠3[/latex] and [latex]∠6[/latex] are alternate interior angles and have equal measure; [latex]∠4[/latex] and [latex]∠5[/latex] are alternate interior angles and have equal measure as well.
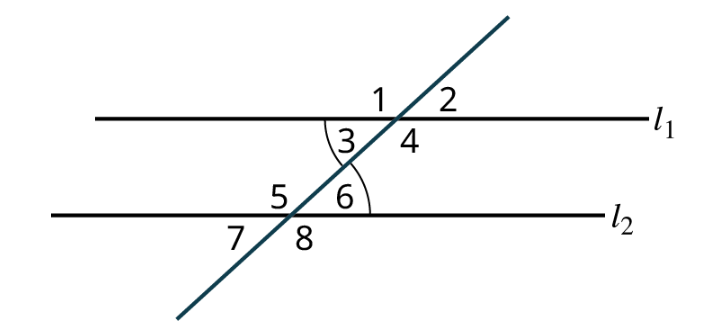
Alternate exterior angles are exterior angles on opposite sides of the transversal and have the same measure. For example in the image below, [latex]∠2[/latex] and [latex]∠7[/latex] are alternate exterior angles and have equal measures; [latex]∠1[/latex] and [latex]∠8[/latex] are alternate exterior angles and have equal measures as well.
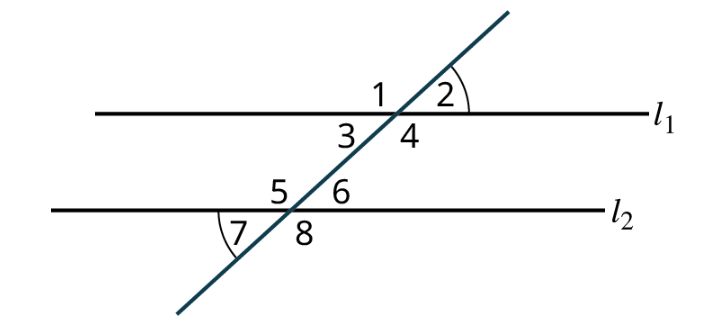
Corresponding angles refer to one exterior angle and one interior angle on the same side as the transversal, which have equal measures. In the image below, [latex]∠1[/latex] and [latex]∠5[/latex] are corresponding angles and have equal measures; [latex]∠3[/latex] and [latex]∠7[/latex] are corresponding angles and have equal measures; [latex]∠2[/latex] and [latex]∠6[/latex] are corresponding angles and have equal measures; [latex]∠4[/latex] and [latex]∠8[/latex] are corresponding angles and have equal measures as well.
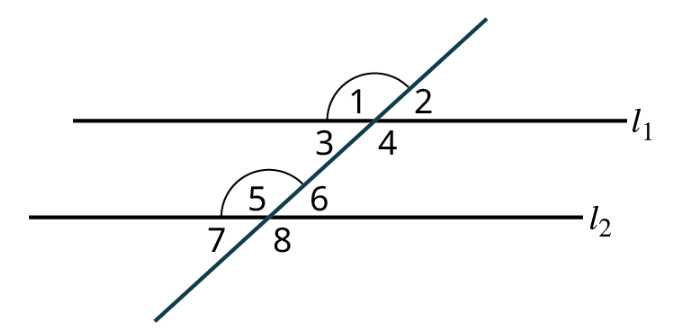
transversals, alternate interior angles, alternate exterior angles, and corresponding angles
A transversal is a line that intersects two or more other lines, creating various angles. Alternate interior angles are a pair of angles that lie on opposite sides of the transversal and are on the inside of the two other lines. These angles are equal in measure. Alternate exterior angles are a pair of angles that lie on opposite sides of the transversal and are on the outside of the two other lines. These angles are equal in measure. Corresponding angles are a pair of angles that are in the same relative position with respect to the transversal, but they are on different intersected lines. These angles are also equal in measure.