- Identify and explain points, lines, and planes
- Measure angles using degrees and radians
- Determine the supplement and complement of an angle
- Calculate angles formed by transversals intersecting parallel lines
Points, Lines, and Planes
The Main Idea
A point is a location in space with no length, width, or height.
A line is an infinite collection of points extending infinitely in both directions.
A line segment is a finite portion of a line with two endpoints.
A ray is a part of a line that starts at an endpoint and extends infinitely in one direction.
Parallel lines are lines that lie in the same plane and move in the same direction, but never intersect.
Two lines that intersect at a [latex]90^\circ[/latex] angle are perpendicular lines.
The properties of planes include:
- Three points including at least one noncollinear point determine a plane.
- A line and a point not on the line determine a plane.
- The intersection of two distinct planes is a straight line.
You can view the transcript for “Math Antics – Points, Lines, & Planes” here (opens in new window).
Angle Basics
The Main Idea
An angle is formed when two lines, line segments, or rays meet at a common point called the vertex. The two lines or segments that form the angle are called the sides of the angle.
Measurement: Angles are measured in degrees ([latex]°[/latex]) or radians. We use a protractor to measure the size of an angle.
Types of Angles:
- Right Angle: A right angle measures exactly [latex]90[/latex] degrees. It forms a perfect “L” shape.
- Acute Angle: An acute angle measures less than [latex]90[/latex] degrees. It is smaller than a right angle. A key to remember acute angles is a small angle is “a cute” little angle.
- Obtuse Angle: An obtuse angle measures more than [latex]90[/latex] degrees but less than [latex]180[/latex] degrees. It is larger than a right angle.
- Straight Angle: A straight angle measures exactly [latex]180[/latex] degrees. It forms a straight line.
- Reflex Angle: A reflex angle measures more than [latex]180[/latex] degrees but less than [latex]360[/latex] degrees. It is larger than a straight angle.
The following video explores four of the five angle types.
You can view the transcript for “Types of Angles | Obtuse, Acute, Right, & Straight Angles” here (opens in new window).
Measuring Angles
Watch the following video for more on how to use a protractor.
You can view the transcript for “How to use a protractor” here (opens in new window).
Degrees versus Radians
The Main Idea
Degrees are the most common measurement of angles. A circle is divided into [latex]360^\circ[/latex]. The symbol for degrees is a small, raised circle: [latex]^\circ[/latex].
Radians are an alternative unit of angle measurement. In a circle, there are [latex]2π[/latex] radians, where [latex]π[/latex] (pi) is approximately [latex]3.14[/latex]. The symbol for radians is [latex]\text{rad}[/latex].
The conversion factor between degrees and radians is [latex]\frac{180}{π}[/latex].
[latex]\text{Angle in Degrees} = \text{Angle in Radians }\times\frac{180}{π}[/latex]
[latex]\text{Angle in Radians} = \text{Angle in Degrees }\times\frac{π}{180}[/latex]
Degrees are commonly used in everyday situations like navigation, construction, and basic geometry, while radians are more prevalent in advanced mathematics, physics, engineering, and other scientific fields.
You can view the transcript for “Radians and Degrees (NancyPi)” here (opens in new window).
Supplementary and Complementary Angles
The Main Idea
Supplementary Angles: Two angles are considered supplementary when the sum of their measures is equal to 180 degrees. In other words, if you have two angles, and when you add their measures together, the result is 180 degrees, then those angles are supplementary.
Complementary Angles: Two angles are considered complementary when the sum of their measures is equal to 90 degrees. In other words, if you have two angles, and when you add their measures together, the result is 90 degrees, then those angles are complementary.
You can view the transcript for “Complementary and Supplementary Angles | How to Find Missing Angles | Math with Mr. J” here (opens in new window).
In the following video we show more examples of how to find the supplement and complement of an angle.
You can view the transcript for “Determine the Complement and Supplement of a Given Angle” here (opens in new window).
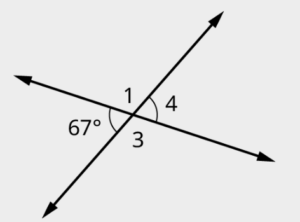
Vertical Angles
The Main Idea
Vertical angles are a pair of opposite angles that are formed when two lines intersect. These angles are located across from each other and share a common vertex or point of intersection. Vertical angles have equal measures, which means they have the same angle measurement.
You can view the transcript for “What are Vertical Angles? | Math with Mr. J” here (opens in new window).
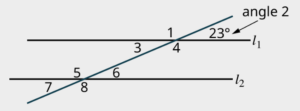
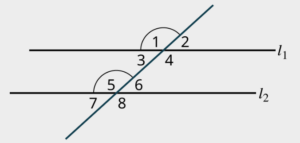
Transversals
The Main Idea
A transversal is a line that intersects two or more other lines. It cuts across these lines at different points, creating various angles.
Alternate interior angles are a pair of angles that lie on opposite sides of the transversal and are on the inside of the two other lines. These angles are equal in measure.
Alternate exterior angles are a pair of angles that lie on opposite sides of the transversal and are on the outside of the two other lines. These angles are equal in measure.
Corresponding angles are a pair of angles that are in the same relative position with respect to the transversal, but they are on different intersected lines. These angles are also equal in measure.
You can view the transcript for “Parallel Lines cut by a Transversal” here (opens in new window).