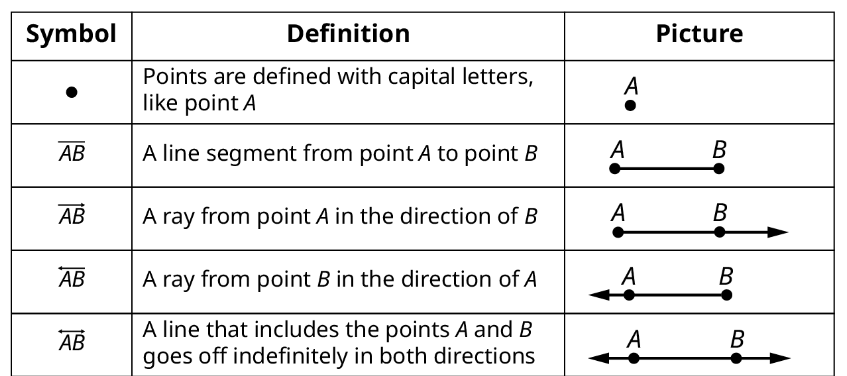
- Identify and explain points, lines, and planes
- Measure angles using degrees and radians
- Determine the supplement and complement of an angle
- Calculate angles formed by transversals intersecting parallel lines
Points, Lines, and Planes
Points, Lines, Line segments, and Rays
In this section, we will begin our exploration of geometry by looking at the basic definitions of a point, line, line segment, and ray.
A point is an indivisible location which has no width, length, or breadth. It is the most basic and fundamental element. It is often represented by a dot or a small mark and has no size, shape, or dimension. A point is considered to be location in space and serves as a reference for describing other geometric objects such as lines, segments, and shapes.
A line is an infinitely long and straight path in both directions. It extends infinitely in both directions without an endpoint. It is denoted by a line with arrows at both ends. A line can be thought of as a collection of infinite points that lie on the same straight path.
A line segment is a portion of a line with two distinct endpoints. It has a finite length and does not extend infinitely in both directions like a line. It is represented by a line segment with a small filled in circle on each end to indicate the endpoints.
A ray is a part of a line that starts at a specific point, called the endpoint, and extends infinitely in one direction. It is represented by a line with an endpoint and an arrow indicating the direction of the ray. Rays can be named by using their endpoint and any other point on the ray.
lines, line segments, and rays
- A point is a location in space with no length, width, or height.
- A line is an infinite collection of points extending infinitely in both directions.
- A line segment is a finite portion of a line with two endpoints.
- A ray is a part of a line that starts at an endpoint and extends infinitely in one direction.
Let’s examine these core geometric elements to understand their notation and see how they are graphically represented.
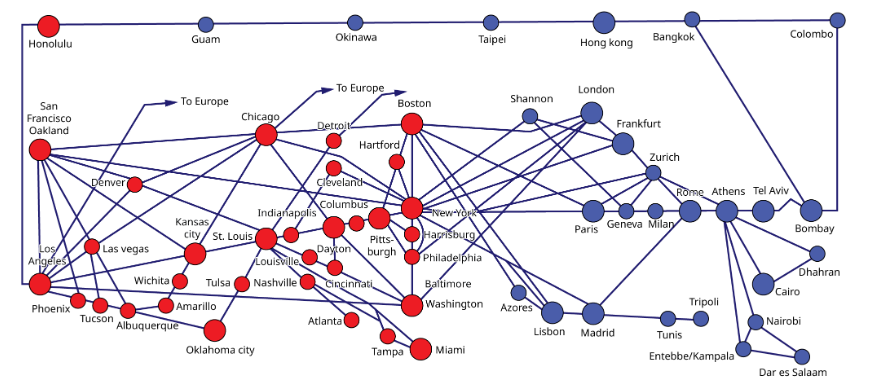
There are numerous applications of line segments in daily life. For example, airlines working out routes between cities, where each city’s airport is a point, and the points are connected by line segments. Another example is a city map. Think about the intersection of roads, such that the center of each intersection is a point and the points are connected by line segments representing the roads.

For the line given above, define:
- [latex]\overline{\rm DE}[/latex]
- [latex]F[/latex]
- [latex]\overleftrightarrow{\rm DF}[/latex]
- [latex]\overline{\rm EF}[/latex]
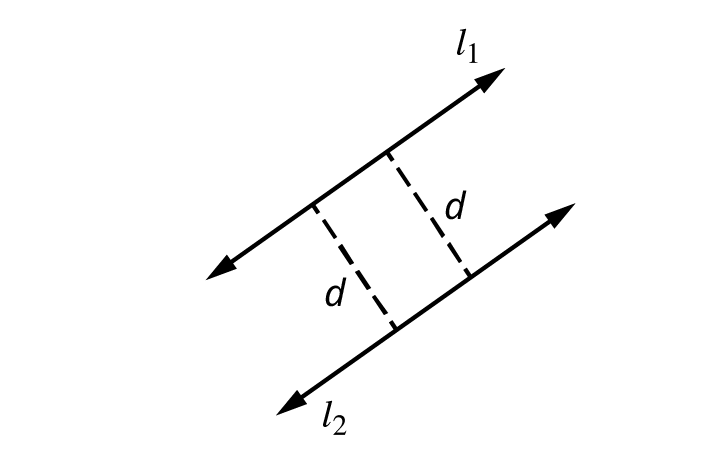
Parallel Lines
Parallel lines are lines that lie in the same plane and move in the same direction, but never intersect. To indicate that the line [latex]l_1[/latex] and the line [latex]l_2[/latex] are parallel we often use the symbol [latex]l_1 ∥ l_2[/latex]. The distance [latex]d[/latex] between parallel lines remains constant as the lines extend infinitely in both directions.
parallel lines
Parallel lines are lines in the same plane that never meet, no matter how long they extend, and they are always the same distance apart. We use the symbol [latex]∥[/latex] to show that two lines are parallel.
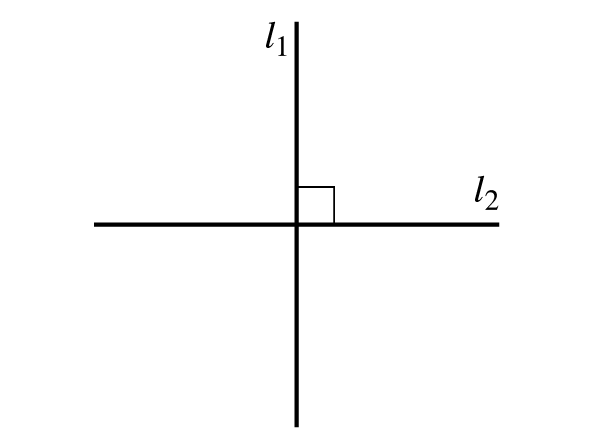
Perpendicular Lines
Two lines that intersect at a [latex]90^\circ[/latex] angle are perpendicular lines and are symbolized by [latex]⊥[/latex]. If [latex]l_1[/latex] and [latex]l_2[/latex] are perpendicular, we write [latex]l_1 ⊥ l_2[/latex]. When two lines form a right angle, a [latex]90^\circ[/latex] angle, we symbolize it with a little square [latex]□[/latex].
perpendicular lines
Perpendicular lines are two lines that meet to form a right angle, marked by [latex]⊥[/latex]. We use a small square to show this [latex]90^\circ[/latex] angle where they intersect.
Planes
In geometry, a plane is one of the most fundamental concepts, representing a flat, two-dimensional surface that extends infinitely in all directions. It’s like a vast sheet of paper with no edges and no thickness.
planes
A plane is a two-dimensional surface with infinite length, infinite width, and no thickness.
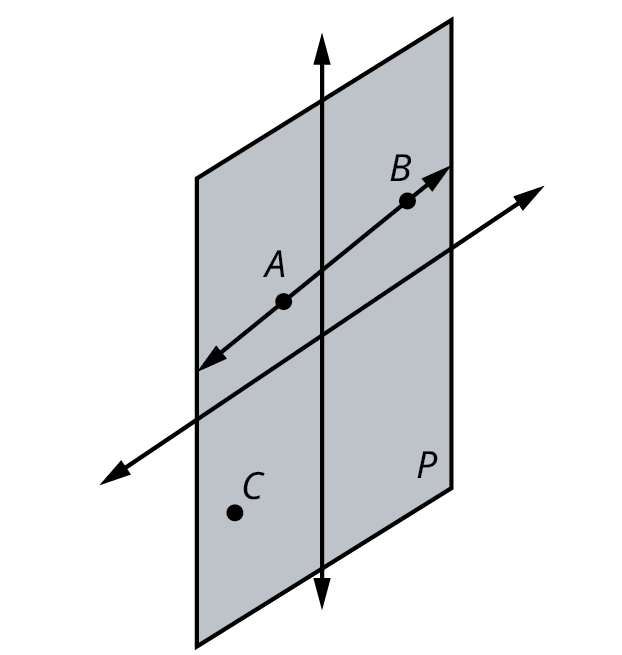
We also identify a plane by three noncollinear points, or points that do not lie on the same line. Think of a piece of paper, but one that has infinite length, infinite width, and no thickness. However, not all planes must extend infinitely. Sometimes a plane has a limited area. We usually label planes with a single capital letter, such as Plane [latex]P[/latex], as shown in the figure below, or by all points that determine the edges of a plane. In the following figure, Plane [latex]P[/latex] contains points [latex]A[/latex] and [latex]B[/latex], which are on the same line, and point [latex]C[/latex], which is not on that line. By definition, [latex]P[/latex] is a plane. We can move laterally in any direction on a plane.
One plane you have probably seen a lot is the Cartesian coordinate system with the [latex]x[/latex]-axis marked off in horizontal units, and [latex]y[/latex]-axis marked off in vertical units. In the Cartesian plane, we can identify the different types of lines as they are positioned in the system, as well as their locations.

properties of planes
The properties of planes include:
- Three points including at least one noncollinear point determine a plane.
- A line and a point not on the line determine a plane.
- The intersection of two distinct planes is a straight line.