Similar Triangles
When we use a map to plan a trip, a sketch to build a bookcase, or a pattern to sew a dress, we are working with similar figures. In geometry, if two figures have exactly the same shape but different sizes, we say they are similar figures. One is a scale model of the other. The corresponding sides of the two figures have the same ratio, and all their corresponding angles are have the same measures.
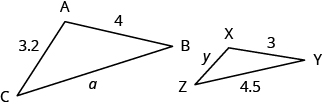
The two triangles below are similar. Each side of [latex]\Delta ABC[/latex] is four times the length of the corresponding side of [latex]\Delta XYZ[/latex] and their corresponding angles have equal measures.
[latex]\Delta ABC[/latex] and [latex]\Delta XYZ[/latex] are similar triangles. Their corresponding sides have the same ratio and the corresponding angles have the same measure.
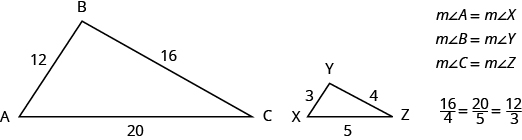
properties of similar triangles
If two triangles are similar, then their corresponding angle measures are equal and their corresponding side lengths are in the same ratio.
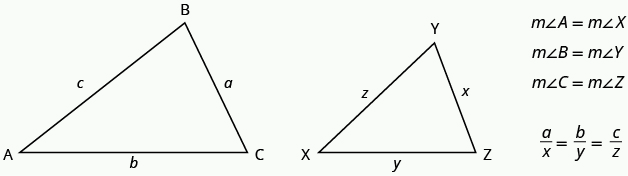
The length of a side of a triangle may be referred to by its endpoints, two vertices of the triangle. For example, in [latex]\Delta ABC\text{:}[/latex]
[latex]\begin{array}{c}\text{the length }a\text{ can also be written }BC\hfill \\ \text{the length }b\text{ can also be written }AC\hfill \\ \text{the length }c\text{ can also be written }AB\hfill \end{array}[/latex]
We will often use this notation when we solve similar triangles because it will help us match up the corresponding side lengths.
We can use the notion that triangles are similar to solve for an unknown side length.
How To: Find the Unknown Side Length in a Triangle When Given Similar Triangles
To find an unknown side length in a triangle when given similar triangles, you can use the concept of proportional relationships between corresponding sides. Below are steps to follow when solving for an unknown side given similar triangles. We will use the following triangles to demonstrate these steps:
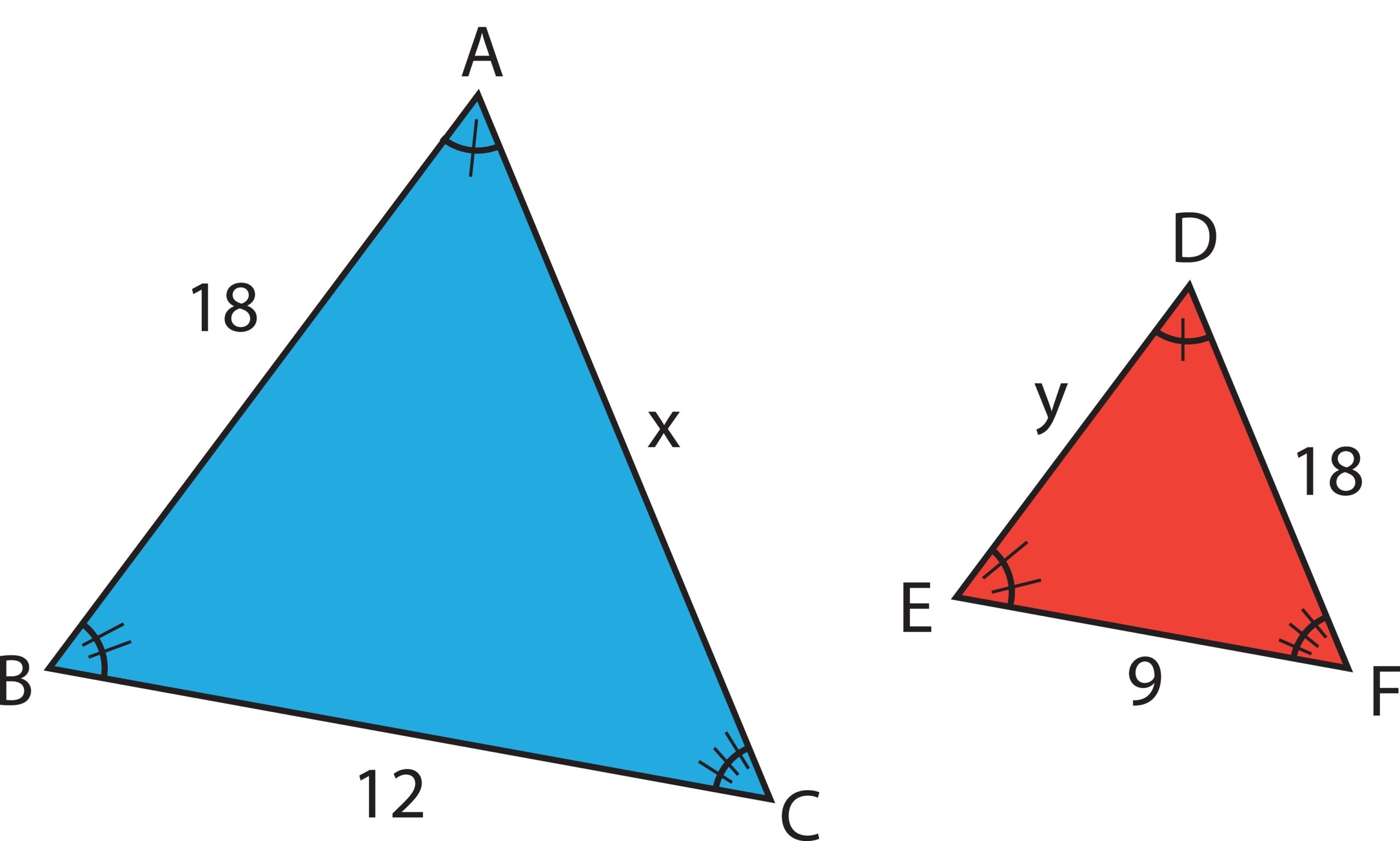
- Identify the corresponding sides in the two similar triangles.
- [latex]AB \sim ED, BC \sim EF, CA \sim FD[/latex]
- Write the ratio of the lengths of the corresponding sides.
- [latex]\frac{AB}{ED} = \frac{BC}{EF} = \frac{CA}{FD}[/latex]
- Set up a proportion to solve for the unknown.
- [latex]\frac{AB}{ED} = \frac{BC}{EF}[/latex]
- [latex]\frac{18}{x} = \frac{12}{9}[/latex]
- Solve the proportion by cross multiplying and dividing to find the unknown
- [latex]AB*EF = BC*ED[/latex]
- [latex]18*9 = 12*x[/latex]
- [latex]\frac{18*9}{12} =x[/latex]
Here is an example for you to try.