- Classify triangles based on their angles and side lengths
- Determine the measure of the third angle in a triangle when the measures of two angles are given
- Apply properties of similar triangles to find unknown side lengths
- Use the Pythagorean theorem to calculate unknown side lengths in triangles
Types of Triangles
The Main Idea
Triangles are one of the fundamental shapes in geometry. They can be classified based on their angle measures and side lengths. These two components help us categorize and understand different types of triangles.
- Classification by Side Lengths:
- Equilateral Triangle: An equilateral triangle has all three sides of equal length. Consequently, all three angles are also equal, measuring 60 degrees each.
- Isosceles Triangle: An isosceles triangle has two sides of equal length. This means two of its angles are also equal.
- Scalene Triangle: A scalene triangle has no sides of equal length. Consequently, all three angles are different from one another.
- Classification by Angle Measures:
- Right Triangle: A right triangle has one angle measuring exactly 90 degrees.
- Acute Triangle: An acute triangle has all three angles measuring less than 90 degrees.
- Obtuse Triangle: An obtuse triangle has one angle measuring greater than 90 degrees.
You can view the transcript for “What are the Different Types of Triangles? | Don’t Memorise” here (opens in new window).
Finding the Measure of the Third Angle in a Triangle
The Main Idea
Finding the measure of the third angle in a triangle involves determining the value of the remaining angle when the measures of two angles are known. Remember all angles in a triangle add up to equal [latex]180^{\circ}[/latex].
To find the measure of the third angle in a triangle:
- Add the measures of the two known angles together.
- Subtract the sum from [latex]180[/latex] degrees.
- The resulting value is the measure of the third angle.
You can view the transcript for “Missing Angles in Triangles | How to Find the Missing Angle of a Triangle Step by Step” here (opens in new window).
Similar Triangles
The Main Idea
Finding similar triangles involves comparing the corresponding angles and side lengths of two or more triangles to determine if they have proportional relationships.
To determine if triangles are similar:
- Compare the measures of their corresponding angles. If all angles have the same measures, the triangles are similar.
- Compare the lengths of their corresponding sides. If the ratios of the corresponding side lengths are equal, the triangles are similar.
To solve for an unknown side of a triangle given two similar triangles we use the following steps:
- Identify the corresponding sides in the two similar triangles.
- Write the ratio of the lengths of the corresponding sides.
- Set up a proportion to solve for the unknown.
- Solve the proportion by cross multiplying and dividing to find the unknown.
You can view the transcript for “When are Two Triangles Similar? | Don’t Memorise” here (opens in new window).
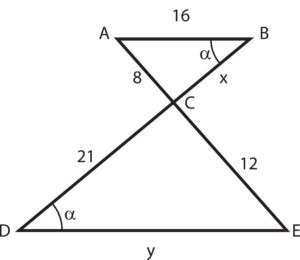
In the video below we show an example of how to find the missing sides of two triangles that are similar.
You can view the transcript for “Ex 1: Find the Length of a Side of a Triangle Using Similar Triangles” here (opens in new window).
Using the Pythagorean Theorem
The Main Idea
The Pythagorean Theorem is a fundamental concept in geometry that relates to the relationship between the sides of a right triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
In equation form, the Pythagorean Theorem can be written as: [latex]c^2 = a^2 + b^2[/latex]
Where [latex]c[/latex] represents the length of the hypotenuse, and [latex]a[/latex] and [latex]b[/latex] represent the lengths of the other two sides (called the legs) of the right triangle.
To use the Pythagorean Theorem, you can follow these steps:
- Identify the right triangle: Ensure that you have a triangle with a right angle ([latex]90^\circ[/latex]).
- Identify the legs and hypotenuse: Label the lengths of the legs as [latex]a[/latex] and [latex]b[/latex], and the length of the hypotenuse as [latex]c[/latex] .
- Apply the Pythagorean Theorem: Square the lengths of the legs ([latex]a^2[/latex] and [latex]b^2[/latex]), then add them together. The result should be equal to the square of the length of the hypotenuse ([latex]c^2[/latex]).
- Solve for the unknown: If you know the lengths of two sides (legs or hypotenuse), you can use the theorem to find the length of the remaining side by rearranging the equation and solving for the unknown value.
You can view the transcript for “An Introduction to the Pythagorean Theorem | Math with Mr. J” here (opens in new window).
In the following video we show two more examples of how to use the Pythagorean Theorem to solve application problems.
You can view the transcript for “Solve Applications Using the Pythagorean Theorem (c only)” here (opens in new window).