- Identify whole numbers and counting numbers
- Write whole numbers in words
- Round whole numbers
- Add, subtract, multiply, and divide whole numbers
Identify Counting Numbers and Whole Numbers
In elementary mathematics, we frequently use the most fundamental set of numbers, which we typically employ for counting objects: [latex]1, 2, 3, 4, 5, ...[/latex] and so forth. These numbers are referred to as the counting numbers. The discovery of the number zero was a big step in the history of mathematics. Including zero with the counting numbers gives a new set of numbers called the whole numbers.
Whole and Counting Numbers
Counting numbers start with [latex]1[/latex] and continue.
Whole numbers are the counting numbers and zero.
Modeling Numbers and Number Lines
Counting numbers and whole numbers can be visualized on a number line, as shown below. The numbers on the number line increase from left to right, and decrease from right to left. The point labeled [latex]0[/latex] is called the origin. The points are equally spaced to the right of [latex]0[/latex] and labeled with the counting numbers.

Our number system is called a place value system because the value of a digit depends on its position, or place, in a number. The number [latex]537[/latex] has a different value than the number [latex]735[/latex]. Even though they use the same digits, their value is different because of the different placement of the [latex]3[/latex],[latex]7[/latex], and the [latex]5[/latex].
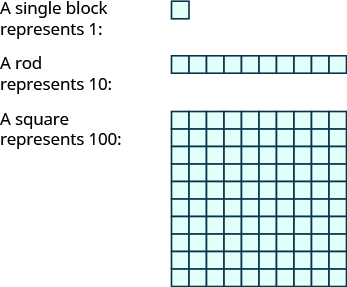
Base-[latex]10[/latex] blocks provide a way to model place value. The blocks can be used to represent hundreds, tens, and ones. Notice in the image below that the tens rod is made up of [latex]10[/latex] ones, and the hundreds square is made of [latex]10[/latex] tens, or [latex]100[/latex] ones.
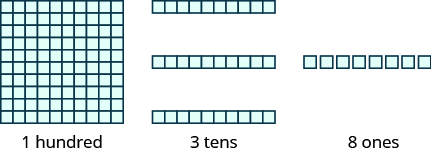
The image below shows the number [latex]138[/latex] modeled with base-[latex]10[/latex] blocks. We can use place value notation to show the value of the number [latex]138[/latex].
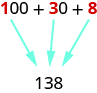
| Digit | Place value | Number | Value | Total value |
|---|---|---|---|---|
| [latex]1[/latex] | hundreds | [latex]1[/latex] | [latex]100[/latex] | [latex]100\phantom{\rule{1 em}{0ex}}[/latex] |
| [latex]3[/latex] | tens | [latex]3[/latex] | [latex]10[/latex] | [latex]30\phantom{\rule{1 em}{0ex}}[/latex] |
| [latex]8[/latex] | ones | [latex]8[/latex] | [latex]1[/latex] | [latex]+\phantom{\rule{.5 em}{0ex}}8\phantom{\rule{1 em}{0ex}}[/latex] |
| [latex]\text{Sum =}138\phantom{\rule{1 em}{0ex}}[/latex] |

Identify the Place Value of a Digit
By looking at base-[latex]10[/latex] blocks, we saw that each place in a number has a different value. A place value chart is a useful way to summarize this information. The place values are separated into groups of three, called periods. The periods are ones, thousands, millions, billions, trillions, and so on. In a written number, commas separate the periods.
Just as with the base-[latex]10[/latex] blocks, where the value of the tens rod is ten times the value of the ones block and the value of the hundreds square is ten times the tens rod, the value of each place in the place-value chart is ten times the value of the place to the right of it.
The chart below shows how the number [latex]5,278,194[/latex] is written in a place value chart.
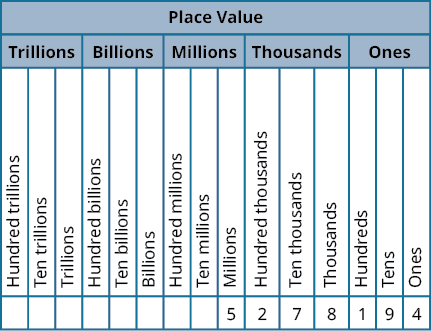
- The digit [latex]5[/latex] is in the millions place. Its value is [latex]5,000,000[/latex].
- The digit [latex]2[/latex] is in the hundred thousands place. Its value is [latex]200,000[/latex].
- The digit [latex]7[/latex] is in the ten thousands place. Its value is [latex]70,000[/latex].
- The digit [latex]8[/latex] is in the thousands place. Its value is [latex]8,000[/latex].
- The digit [latex]1[/latex] is in the hundreds place. Its value is [latex]100[/latex].
- The digit [latex]9[/latex] is in the tens place. Its value is [latex]90[/latex].
- The digit [latex]4[/latex] is in the ones place. Its value is [latex]4[/latex].
