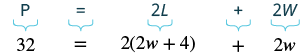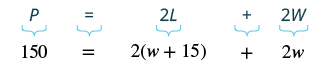Area and Circumference: Fresh Take

Lumen Learning

Area and Circumference: Fresh Take

Find the area of rectangles, triangles, trapezoids, and irregular shapes
Solve real-life area problems involving rectangles, triangles, and trapezoids
Find the circumference and area of circular objects

Find the Perimeter and Area of a Rectangle

The Main Idea

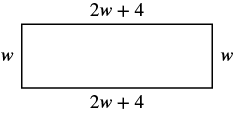
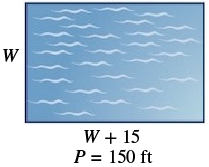
The perimeter of a rectangle is the distance around its outer edge. To find the perimeter, you add up
the lengths of all four sides of the rectangle. If the length of the rectangle is represented by [latex]L[/latex] and
the width by [latex]W[/latex], the formula for calculating the perimeter is [latex]P = 2(L + W)[/latex], where
[latex]P[/latex] represents the perimeter.

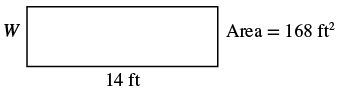
The area of a rectangle is a measurement that tells us the amount of space enclosed by the rectangle.
To find the area, you multiply the length of the rectangle by its width. The formula for calculating the area is
[latex]A = L × W[/latex], where [latex]A[/latex] represents the area.

You can view the transcript for “How to find the Area and Perimeter of a Rectangle” here (opens in new
window).

The area of a rectangular room is [latex]168[/latex] square feet. The length is [latex]14[/latex] feet. What is the width?

The length of a rectangle is four centimeters more than twice the width. The perimeter is [latex]32[/latex] centimeters. Find the length and width.

The perimeter of a rectangular swimming pool is [latex]150[/latex] feet. The length is [latex]15[/latex] feet more than the width. Find the length and width.

Watch this video to see another similar example of finding area given the relationship between the length and width of a rectangle.

You can view the transcript for “Ex: Find the Area of a Rectangle Given the Perimeter” here (opens in
new window).

Find the Area and Perimeter of a Triangle

The Main Idea

The perimeter of a triangle is the total length of its three sides. To find the perimeter, you add up the lengths of all three sides of the triangle. If the lengths of the sides are represented by [latex]a[/latex], [latex]b[/latex], and [latex]c[/latex], the formula for calculating the perimeter is [latex]P = a + b + c[/latex], where [latex]P[/latex] represents the perimeter.

The area of a triangle is a measurement that tells us the amount of space enclosed by the triangle. To find the area, you multiply the base of the triangle by its corresponding height and divide the product by [latex]2[/latex]. The formula for calculating the area is [latex]A = \frac{1}{2} × b × h[/latex], where [latex]A[/latex] represents the area, [latex]b[/latex] represents the base, and [latex]h[/latex] represents the height.

You can view the transcript for “How to Find the Area and Perimeter of a Triangle” here (opens in new
window).

The following video provides another example of how to use the area formula for triangles.

You can view the transcript for “Ex: Find the Area of a Triangle (Whole Number)” here (opens in new
window).

In our next video, we show an example of how to find the height of a triangle given it’s area.

You can view the transcript for “Ex: Find the Height of a Triangle Given Area (Even Base)” here (opens
in new window).

The perimeter of an equilateral triangle is [latex]93[/latex] inches. Find the length of each side.

Find the Area of a Trapezoid

The Main Idea

A trapezoid is a quadrilateral with one pair of parallel sides.

To find the area of a trapezoid, you multiply the sum of the lengths of the parallel sides (base1 ([latex]b[/latex]) and base2 ([latex]B[/latex])) by the height ([latex]h[/latex]) and divide the result by [latex]2[/latex]. The formula for calculating the area of a trapezoid is [latex]A = \frac{(b + B) × h}{2}[/latex], where [latex]A[/latex] represents the area. This can also be written as: [latex]{\text{Area}}_{\text{trapezoid}}=\Large\frac{1}{2}\normalsize h\left(b+B\right)[/latex]

You can view the transcript for “Area of a Trapezoid | MathHelp.com” here (opens in new window).

In the next video we show another example of how to use the formula to find the area of a trapezoid given the
lengths of it’s height and bases.

You can view the transcript for “Ex: Find the Area of a Trapezoid” here (opens in new window).

Find the area of a trapezoid whose height is [latex]5[/latex] feet and whose bases are [latex]10.3[/latex] and [latex]13.7[/latex] feet.

Find the Circumference and Area of Circles

The Main Idea

The circumference of a circle is the distance around its outer edge or boundary. The formula for calculating the circumference of a circle is [latex]C = 2πr[/latex] or [latex]C = πd[/latex], where [latex]C[/latex] represents the circumference, [latex]r[/latex] represents the radius, and [latex]d[/latex] represents the diameter.

The area of a circle is a measurement that tells us the amount of space enclosed by the circle. The formula for calculating the area of a circle is [latex]A = πr^2[/latex], where [latex]A[/latex] represents the area, and [latex]r[/latex] represents the radius.

You can view the transcript for “Math Antics – Circles, Circumference And Area” here (opens in new
window).

A circle has radius [latex]10[/latex] centimeters. Approximate its:

circumference
area

A circle has a diameter of [latex]14.6[/latex] inches. Approximate its:

circumference
area

Watch the following video to see another example of how to find the circumference of a circle.

You can view the transcript for “Examples: Determine the Circumference of a Circle” here (opens in new
window).

In the next video example, we find the area of a circle.

You can view the transcript for “Example: Determine the Area of a Circle” here (opens in new
window).

Find the Area of Irregular Figures

To find the area of an irregular figure, you break it down into simpler shapes whose areas can be calculated. For
example, you can divide the irregular figure into rectangles, triangles, squares, circles, or other familiar shapes.
Then, calculate the area of each individual shape using the appropriate formulas. Once you have found the areas of the
simpler shapes, add them together to find the total area of the irregular figure. Keep in mind that this method works
best when the irregular figure can be divided into known shapes.

The following video gives an example of how to find the area of an “L” shaped polygon using the dimensions of two
rectangles.

You can view the transcript for “Ex: Find the Area of an L-Shaped Polygon Involving Whole Numbers”
here (opens in new window).

The next video example find the area of an object containing one semi-circle and a rectangle.

You can view the transcript for “Example: Determine an Area Involving a Rectangle and Circle” here
(opens in new window).

The next video shows more example of finding the area of irregular shapes.

You can view the transcript for “Area and Perimeter of Irregular Shapes – Tons of Examples!” here
(opens in new window).

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the width of a rectangular room
Step 3. Name. Choose a variable to represent it.	Let W = width
Step 4. Translate. Write the appropriate formula and substitute in the given information.	[latex]A=LW[/latex] [latex]168=14W[/latex]
Step 5. Solve the equation.	[latex]\Large\frac{168}{14}\normalsize= \Large\frac{14W}{14}[/latex] [latex]12=W[/latex]
Step 6. Check: [latex]A=LW[/latex] [latex]168\stackrel{?}{=}14\cdot 12[/latex] [latex]168=168\checkmark[/latex]
Step 7. Answer the question.	The width of the room is [latex]12[/latex] feet.

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the length and width
Step 3. Name. Choose a variable to represent it.	let W = width The length is four more than twice the width. [latex]2w+4[/latex] = length
Step 4. Translate. Write the appropriate formula and substitute in the given information.
Step 5. Solve the equation.	[latex]32=4w+8+2w[/latex] [latex]32=6w+8[/latex] [latex]24=6w[/latex] [latex]4=w[/latex] (width) [latex]2w+4=[/latex] length [latex]2(\color{red}{4})+4[/latex] [latex]8+4=12[/latex] The length is [latex]12[/latex]cm.
Step 6. Check: [latex]P=2L+2W[/latex] [latex]P\stackrel{?}{=}2\cdot 12+2\cdot 4[/latex] [latex]32=32\quad\checkmark[/latex]
Step 7. Answer the question.	The length is [latex]12[/latex] cm and the width is [latex]4[/latex] cm.

Step 1. Read the problem. Draw the figure and label it with the given information.
Step 2. Identify what you are looking for.	the length and width of the pool
Step 3. Name. Choose a variable to represent it. The length is [latex]15[/latex] feet more than the width.	Let [latex]W=\text{width}[/latex] [latex]W+15=\text{length}[/latex]
Step 4. Translate. Write the appropriate formula and substitute.
Step 5. Solve the equation.	[latex]150=2w+30+2w[/latex] [latex]150=4w+30[/latex] [latex]120=4w[/latex] [latex]30=w[/latex] the width of the pool. [latex]w+15[/latex] the length of the pool. [latex]\color{red}{30}+15[/latex] [latex]45[/latex]
Step 6. Check: [latex]P=2L+2W[/latex] [latex]150\stackrel{?}{=}2(45)+2(30)[/latex] [latex]150=150\checkmark[/latex]
Step 7. Answer the question.	The length of the pool is [latex]45[/latex] feet and the width is [latex]30[/latex] feet.

Step 1. Read the problem. Draw the figure and label it with the given information.	Perimeter = [latex]93[/latex] in.
Step 2. Identify what you are looking for.	length of the sides of an equilateral triangle
Step 3. Name. Choose a variable to represent it.	Let s = length of each side
Step 4. Translate. Write the appropriate formula. Substitute.
Step 5. Solve the equation.	[latex]93=3s[/latex] [latex]31=s[/latex]
Step 6. Check: [latex]93\stackrel{?}{=}31+31+31[/latex] [latex]93=93\quad\checkmark[/latex]
Step 7. Answer the question.	Each side is [latex]31[/latex] inches.

Step 1. Read the problem. Draw the figure and label it with the given information.
Step 2. Identify what you are looking for.	the area of the trapezoid
Step 3. Name. Choose a variable to represent it.	Let A = the area
Step 4. Translate. Write the appropriate formula. Substitute.
Step 5. Solve the equation.	[latex]A={\Large\frac{1}{2}}\normalsize\cdot 5(24)[/latex] [latex]A=12(5)[/latex] [latex]A=60[/latex] square feet
Step 6. Check: Is this answer reasonable? The area of the trapezoid should be less than the area of a rectangle with base [latex]13.7[/latex] and height [latex]5[/latex], but more than the area of a rectangle with base [latex]10.3[/latex] and height [latex]5[/latex].	[latex]\checkmark[/latex]
Step 7. Answer the question.	The area of the trapezoid is [latex]60[/latex] square feet.

Find the circumference when [latex]r=10[/latex].
Write the formula for circumference.	[latex]C=2\pi \mathit{\text{r}}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi[/latex] and 10 for , [latex]r[/latex] .	[latex]C\approx 2\left(3.14\right)\left(10\right)[/latex]
Multiply.	[latex]C\approx 62.8\text{ centimeters}[/latex]

Find the area when [latex]r=10[/latex].
Write the formula for area.	[latex]A=\pi {\mathit{\text{r}}}^{2}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi[/latex] and 10 for [latex]r[/latex] .	[latex]A\approx \left(3.14\right){\text{(}10\text{)}}^{2}[/latex]
Multiply.	[latex]A\approx 314\text{ square centimeters}[/latex]

Find the circumference when [latex]d=14.6[/latex]
Write the formula for circumference.	[latex]C=\pi \mathit{\text{d}}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi[/latex] and [latex]14.6[/latex] for [latex]d[/latex]	[latex]C\approx \left(3.14\right)\left(14.6\right)[/latex]
Multiply.	[latex]C\approx 45.844\text{ inches}[/latex]

Find the area when [latex]d=14.6[/latex]. We know [latex]d=2r[/latex] so for this problem [latex]r=7.3[/latex]
Write the formula for area.	[latex]A=\pi {\mathit{\text{r}}}^{2}[/latex]
Substitute [latex]3.14[/latex] for [latex]\pi[/latex] and [latex]7.3[/latex] for [latex]r[/latex] .	[latex]A\approx \left(3.14\right){\text{(}7.3\text{)}}^{2}[/latex]
Multiply.	[latex]A\approx 171.915\text{ square inches}[/latex]