Finding the Volume of a Cone
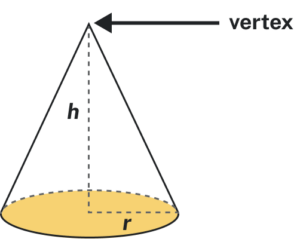
The first image that many of us have when we hear the word ‘cone’ is an ice cream cone. There are many other applications of cones (but most are not as tasty as ice cream cones). In geometry, a cone is a solid figure with one circular base and a vertex. The height of a cone is the distance between its base and the vertex. The cones that we will look at in this section will always have the height perpendicular to the base.
Earlier in this section, we saw that the volume of a cylinder is [latex]V=\pi{r}^{2}h[/latex]. We can think of a cone as part of a cylinder. The image below shows a cone placed inside a cylinder with the same height and same base. If we compare the volume of the cone and the cylinder, we can see that the volume of the cone is less than that of the cylinder.
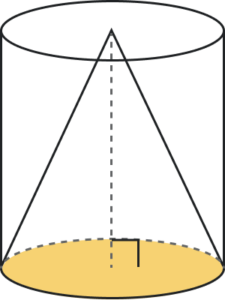
In fact, the volume of a cone is exactly one-third of the volume of a cylinder with the same base and height. The volume of a cone is:
Since the base of a cone is a circle, we can substitute the formula of area of a circle, [latex]\pi{r}^{2}[/latex], for [latex]B[/latex] to get the formula for volume of a cone.
In this book, we will only find the volume of a cone, and not its surface area.
volume of a cone
For a cone with radius [latex]r[/latex] and height [latex]h[/latex].

