Graph Theory Basics: Learn It 1

  • Recognize graph components: vertices, edges, loops, and vertex degrees
  • Identify both a path and a circuit through a graph
  • Determine whether a graph is connected or disconnected
  • Find the shortest path through a graph using Dijkstra’s Algorithm

Drawing Graphs

In the modern world, planning efficient routes is essential for business and industry, with applications as varied as product distribution, laying new fiber optic lines for high-speed internet, and suggesting new friends within social network websites like Facebook. Let’s look at an example of planning an effective route.

Here is a portion of a housing development from Missoula, Montana. As part of her job, the development’s lawn inspector has to walk down every street in the development making sure homeowners’ landscaping conforms to the community requirements.

A map of the streets and houses in the development

 

Naturally, she wants to minimize the amount of walking she has to do. Is it possible for her to walk down every street in this development without having to do any backtracking? While you might be able to answer that question just by looking at the picture for a while, it would be ideal to be able to answer the question for any picture regardless of its complexity.To do that, we first need to simplify the picture into a form that is easier to work with. We can do that by drawing a simple line for each street. Where streets intersect, we will place a dot.

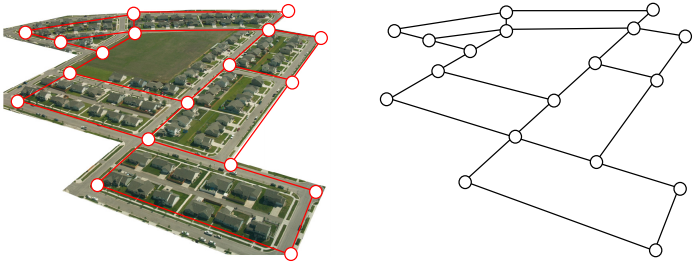
A graph made from a map of streets by drawing an edge where each street is and a vertex where every intersection is.

This type of simplified picture is called a graph.

Graphs, vertices, and edges

A graph consists of a set of dots, called vertices, and a set of edges connecting pairs of vertices.

You probably already noticed that we are using the term graph differently than you may have used the term in the past to describe the graph of a mathematical function.

While we loosely defined some terminology earlier, we now will try to be more specific.

Parts of a graph

vertex

A vertex is a dot in the graph that could represent an intersection of streets, a land mass, or a general location, like “work” or “school”. Vertices are often connected by edges. Note that vertices only occur when a dot is explicitly placed, not whenever two edges cross. Imagine a freeway overpass—the freeway and side street cross, but it is not possible to change from the side street to the freeway at that point, so there is no intersection and no vertex would be placed.

edges

Edges connect pairs of vertices. An edge can represent a physical connection between locations, like a street, or simply that a route connecting the two locations exists, like an airline flight. It is not necessary for the edges in a graph to be straight. In fact, you can draw an edge any way you want.

loop

A loop is a special type of edge that connects a vertex to itself. Loops are not used much in street network graphs.

 

Three vertices connected to each other by edges. One vertex has a loop connecting itself to itself.

degree of a vertex

The degree of a vertex is the number of edges meeting at that vertex. It is possible for a vertex to have a degree of zero or larger.

 

Degree [latex]0[/latex] Degree [latex]1[/latex] Degree [latex]2[/latex] Degree [latex]3[/latex] Degree [latex]4[/latex]
A dot. A dot with one line attached to it. A dot with two lines attached to it. A dot with three lines attached to it. A dot with four lines attached to it.

path

A path is a sequence of vertices such that each vertex is adjacent to the next one. In a path, no vertex is repeated. For example, a path from vertex [latex]A[/latex] to vertex [latex]M[/latex] is shown below. It is one of many possible paths in this graph.

 

Rectangular graph with 12 vertices labeled A through M (without I). A path is drawn from A to M going though the points B, F, G, and H.

circuit

A circuit is a path that begins and ends at the same vertex. A circuit starting and ending at vertex [latex]A[/latex] is shown below.

 

Rectangular graph with 12 vertices labeled A through M (without I). A circuit is drawn, going through the points A, B, F, G, L, L, J, and E.

connected graphs

A graph is connected if there is a path from any vertex to any other vertex. Every graph drawn so far has been connected. The graph below is disconnected; there is no way to get from the vertices on the left to the vertices on the right.

 

A 3x4 graph where there is not a path from every vertex to every other vertex.

weights

Depending upon the problem being solved, sometimes weights are assigned to the edges. The weights could represent the distance between two locations, the travel time, or the travel cost. It is important to note that the distance between vertices in a graph does not necessarily correspond to the weight of an edge.

Not every list of vertices or list of edges makes a path. The order must take into account the way in which the edges and vertices are connected. The list must be a sequence, which means they are in order. No edges or vertices can be skipped and you cannot go off the graph.

The graph below shows [latex]5[/latex] cities. The weights on the edges represent the airfare for a one -way flight between the cities.

a. How many vertices and edges does the graph have?
b. Is the graph connected?
c. What is the degree of the vertex representing LA?
d. If you fly from Seattle to Dallas to Atlanta, is that a path or a circuit?
e. If you fly from LA to Chicago to Dallas to LA, is that a path or a circuit.

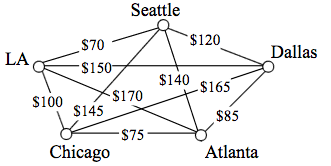
Five dots labeled Seattle, LA, Chicago, Atlanta, and Dallas respectively. Every dot is connected directly to every other dot

When listing the vertices and edges in a graph, work in alphabetical order to avoid accidentally listing the same item twice. When you are finished, count the number of vertices or edges you listed and compare that to the number of vertices or edges on the graph to ensure you didn’t miss any.