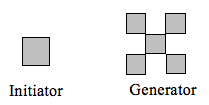
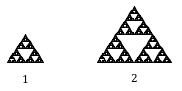Fractal Dimension
In addition to visual self-similarity, fractals exhibit other interesting properties. For example, notice that each step of the Sierpinski gasket iteration removes one quarter of the remaining area. If we remove one quarter of the remaining area indefinitely, we would end up essentially removing all the area on the shape. In other words, we started with a [latex]2[/latex]-dimensional area, and somehow end up with something less than that, but seemingly more than just a [latex]1[/latex]-dimensional line.
To explore this idea, we need to discuss dimension. Something like a line is [latex]1[/latex]-dimensional; it only has length. Any curve is [latex]1[/latex]-dimensional. Things like boxes and circles are [latex]2[/latex]-dimensional, since they have length and width, describing an area. Objects like boxes and cylinders have length, width, and height, describing a volume, and are [latex]3[/latex]-dimensional.
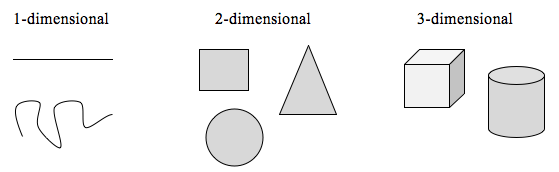
Certain rules apply for scaling objects, related to their dimension.
If we had a line with length [latex]1[/latex], and wanted to scale its length by [latex]2[/latex], we would need two copies of the original line. If we had a line of length [latex]1[/latex], and wanted to scale its length by [latex]3[/latex], we would need three copies of the original.
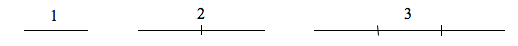
If we had a rectangle with length [latex]2[/latex] and height [latex]1[/latex], and wanted to scale its length and width by [latex]2[/latex], we would need four copies of the original rectangle. If we wanted to scale the length and width by [latex]3[/latex], we would need nine copies of the original rectangle.
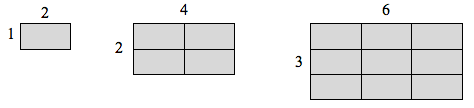
If we had a cubical box with sides of length [latex]1[/latex], and wanted to scale its length and width by [latex]2[/latex], we would need eight copies of the original cube. If we wanted to scale the length and width by [latex]3[/latex], we would need [latex]27[/latex] copies of the original cube.
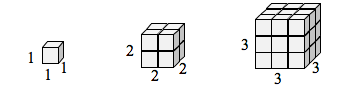
Notice that in the [latex]1[/latex]-dimensional case, copies needed = scale.
In the [latex]2[/latex]-dimensional case, copies needed = scale[latex]^{2}[/latex].
In the [latex]3[/latex]-dimensional case, copies needed = scale[latex]^{3}[/latex].
From these examples, we might infer a pattern.
scaling-dimension relation
To scale a [latex]D[/latex]-dimensional shape by a scaling factor [latex]S[/latex], the number of copies [latex]C[/latex] of the original shape needed will be given by:
Exponential notation
The relation above uses exponential notation. Recall that a number or a variable in a superscript position over a base number or variable is called an exponent. It indicates that the base should be used as a factor a number of times equal to the exponent.
Example: [latex]2^{3}[/latex] indicates to use [latex]2[/latex] as a factor [latex]3[/latex] times.
[latex]2^{3}=2 \ast 2 \ast 2 = 8[/latex].
In the relation above, the equation [latex]C=S^{D}[/latex] indicates that the number of copies of the original shape [latex]C[/latex] can be found by multiplying a scaling factor [latex]S[/latex] by itself the same number of times as the dimension [latex]D[/latex].
scaling-dimension relation to find dimension
To find the dimension [latex]D[/latex] of a fractal, determine the scaling factor [latex]S[/latex] and the number of copies [latex]C[/latex] of the original shape needed, then use the formula:
[latex]D=\frac{\log\left(C\right)}{\log(S)}[/latex]