Constructing a Fractal
We can construct other fractals using a similar approach of recursion. To formalize this a bit, we’re going to introduce the idea of initiators and generators.
initiators and generators
An initiator is a starting shape.
A generator is an arranged collection of scaled copies of the initiator.
To generate fractals from initiators and generators, we follow a simple rule, the fractal generation rule.
fractal generation rule
At each step, replace every copy of the initiator with a scaled copy of the generator, rotating as necessary.
This process is easiest to understand through an example.

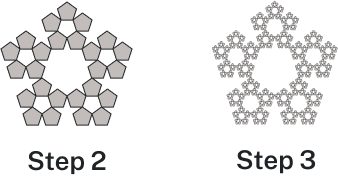
This tells us to, at each step, replace each line segment with the spiked shape shown in the generator. Notice that the generator itself is made up of [latex]4[/latex] copies of the initiator. In step [latex]1[/latex], the single line segment in the initiator is replaced with the generator. For step [latex]2[/latex], each of the four line segments of step [latex]1[/latex] is replaced with a scaled copy of the generator:

This process is repeated to form Step [latex]3[/latex]. Again, each line segment is replaced with a scaled copy of the generator.

Notice that since Step [latex]0[/latex] only had [latex]1[/latex] line segment, Step [latex]1[/latex] only required one copy of Step [latex]0[/latex]. Since Step [latex]1[/latex] had [latex]4[/latex] line segments, Step [latex]2[/latex] required [latex]4[/latex] copies of the generator. Step [latex]2[/latex] then had [latex]16[/latex] line segments, so Step [latex]3[/latex] required [latex]16[/latex] copies of the generator. Step [latex]4[/latex], then, would require [latex]16\cdot4=64[/latex] copies of the generator.
The shape resulting from iterating this process is called the Koch curve, named for Helge von Koch who first explored it in 1904.

Using iteration processes like those above can create a variety of beautiful images evocative of nature. More natural shapes can be created by adding randomness to the steps.

We then repeat this process.

Continuing this process can create mountain-like structures. This landscape[1] was created using fractals, then colored and textured.

Fractals
You can view the transcript for “What Is A Fractal (and what are they good for)?” here (opens in new window).
You can view the transcript for “Fractals are typically not self-similar” here (opens in new window).
You can view the transcript for “How fractals can help you understand the universe | BBC Ideas” here (opens in new window).
- http://en.wikipedia.org/wiki/File:FractalLandscape.jpg ↵