Composition of Functions

1. Find the numbers that make the function in the denominator [latex]g[/latex] equal to zero, and check for any other domain restrictions on [latex]f[/latex] and [latex]g[/latex], such as an even-indexed root or zeros in the denominator.

3. Yes. Sample answer: Let [latex]f\left(x\right)=x+1\text{ and }g\left(x\right)=x - 1[/latex]. Then [latex]f\left(g\left(x\right)\right)=f\left(x - 1\right)=\left(x - 1\right)+1=x[/latex] and [latex]g\left(f\left(x\right)\right)=g\left(x+1\right)=\left(x+1\right)-1=x[/latex]. So [latex]f\circ g=g\circ f[/latex].

7. [latex]\left(f+g\right)\left(x\right)=\frac{4{x}^{3}+8{x}^{2}+1}{2x}[/latex], domain: [latex]\left(-\infty ,0\right)\cup \left(0,\infty \right)[/latex]

[latex]\left(f-g\right)\left(x\right)=\frac{4{x}^{3}+8{x}^{2}-1}{2x}[/latex], domain: [latex]\left(-\infty ,0\right)\cup \left(0,\infty \right)[/latex]

[latex]\left(fg\right)\left(x\right)=x+2[/latex], domain: [latex]\left(-\infty ,0\right)\cup \left(0,\infty \right)[/latex]

[latex]\left(\frac{f}{g}\right)\left(x\right)=4{x}^{3}+8{x}^{2}[/latex], domain: [latex]\left(-\infty ,0\right)\cup \left(0,\infty \right)[/latex]

11. a. 3; b. [latex]f\left(g\left(x\right)\right)=2{\left(3x - 5\right)}^{2}+1[/latex]; c. [latex]f\left(g\left(x\right)\right)=6{x}^{2}-2[/latex]; d. [latex]\left(g\circ g\right)\left(x\right)=3\left(3x - 5\right)-5=9x - 20[/latex]; e. [latex]\left(f\circ f\right)\left(-2\right)=163[/latex]

13. [latex]f\left(g\left(x\right)\right)=\sqrt{{x}^{2}+3}+2,g\left(f\left(x\right)\right)=x+4\sqrt{x}+7[/latex]

25. [latex]\left(1,\infty \right)[/latex]

27. sample: [latex]\begin{cases}f\left(x\right)={x}^{3}\\ g\left(x\right)=x - 5\end{cases}[/latex]

35. sample: [latex]f\left(x\right)=\sqrt{x}[/latex]
[latex]g\left(x\right)=2x+6[/latex]

43. 2

45. 5

59. 9

61. 4

63. 2

73. [latex]f\left(g\left(0\right)\right)=27,g\left(f\left(0\right)\right)=-94[/latex]

91. c. Solve [latex]A\left(m\left(t\right)\right)=4[/latex].

Transformation of Functions

1. A horizontal shift results when a constant is added to or subtracted from the input. A vertical shifts results when a constant is added to or subtracted from the output.

3. A horizontal compression results when a constant greater than 1 is multiplied by the input. A vertical compression results when a constant between 0 and 1 is multiplied by the output.

7. [latex]g\left(x\right)=|x - 1|-3[/latex]

11. The graph of [latex]f\left(x+43\right)[/latex] is a horizontal shift to the left 43 units of the graph of [latex]f[/latex].

15. The graph of [latex]f\left(x\right)+8[/latex] is a vertical shift up 8 units of the graph of [latex]f[/latex].

19. The graph of [latex]f\left(x+4\right)-1[/latex] is a horizontal shift to the left 4 units and a vertical shift down 1 unit of the graph of [latex]f[/latex].

21. decreasing on [latex]\left(-\infty ,-3\right)[/latex] and increasing on [latex]\left(-3,\infty \right)[/latex]

23. decreasing on [latex]\left(0,\infty \right)[/latex]

27.

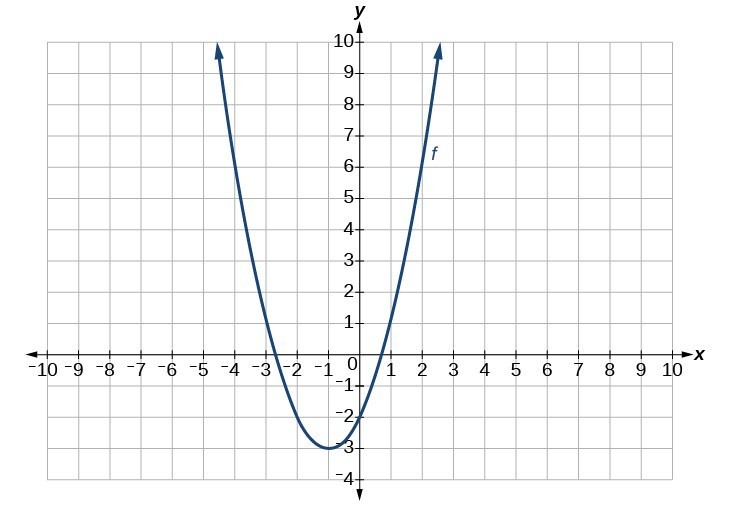
29.

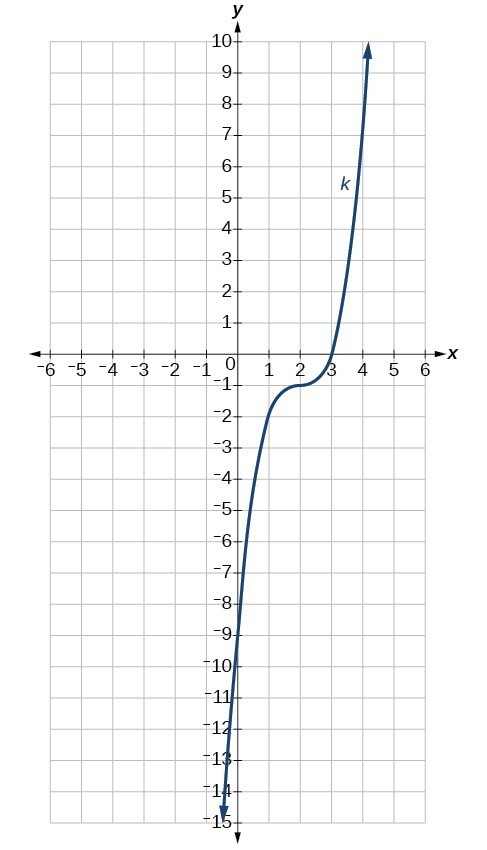
31. [latex]g\left(x\right)=f\left(x - 1\right),h\left(x\right)=f\left(x\right)+1[/latex]

33. [latex]f\left(x\right)=|x - 3|-2[/latex]

35. [latex]f\left(x\right)=\sqrt{x+3}-1[/latex]

39. [latex]f\left(x\right)=|x+3|-2[/latex]

47. even

49. odd

53. The graph of [latex]g[/latex] is a vertical reflection (across the [latex]x[/latex] -axis) of the graph of [latex]f[/latex].

57. The graph of [latex]g[/latex] is a horizontal compression by a factor of [latex]\frac{1}{5}[/latex] of the graph of [latex]f[/latex].

59. The graph of [latex]g[/latex] is a horizontal stretch by a factor of 3 of the graph of [latex]f[/latex].

61. The graph of [latex]g[/latex] is a horizontal reflection across the [latex]y[/latex] -axis and a vertical stretch by a factor of 3 of the graph of [latex]f[/latex].

65. [latex]g\left(x\right)=\frac{1}{3{\left(x+2\right)}^{2}}-3[/latex]

67. [latex]g\left(x\right)=\frac{1}{2}{\left(x - 5\right)}^{2}+1[/latex]

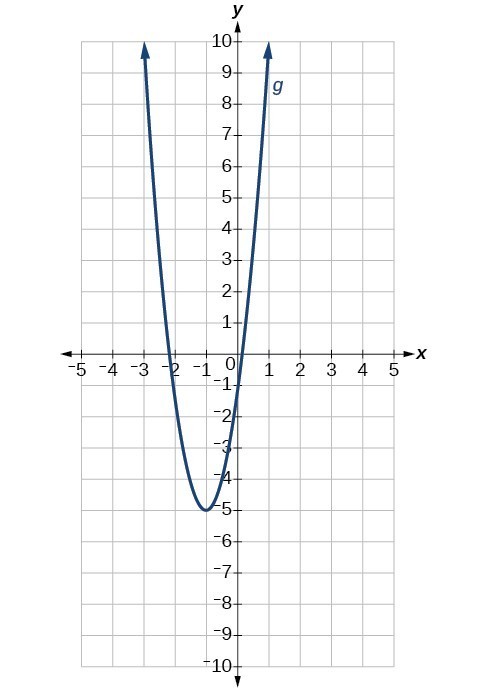
69. The graph of the function [latex]f\left(x\right)={x}^{2}[/latex] is shifted to the left 1 unit, stretched vertically by a factor of 4, and shifted down 5 units.

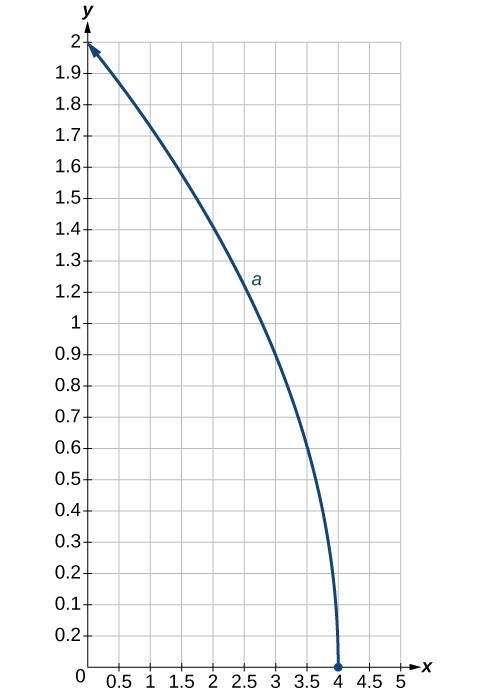
77. The graph of [latex]f\left(x\right)=\sqrt{x}[/latex] is shifted right 4 units and then reflected across the vertical line [latex]x=4[/latex].

Inverse Functions

1. Each output of a function must have exactly one output for the function to be one-to-one. If any horizontal line crosses the graph of a function more than once, that means that [latex]y[/latex] -values repeat and the function is not one-to-one. If no horizontal line crosses the graph of the function more than once, then no [latex]y[/latex] -values repeat and the function is one-to-one.

3. Yes. For example, [latex]f\left(x\right)=\frac{1}{x}[/latex] is its own inverse.

5. Given a function [latex]y=f\left(x\right)[/latex], solve for [latex]x[/latex] in terms of [latex]y[/latex]. Interchange the [latex]x[/latex] and [latex]y[/latex]. Solve the new equation for [latex]y[/latex]. The expression for [latex]y[/latex] is the inverse, [latex]y={f}^{-1}\left(x\right)[/latex].

7. [latex]{f}^{-1}\left(x\right)=x - 3[/latex]

11. [latex]{f}^{-1}\left(x\right)=\frac{-2x}{x - 1}[/latex]

13. domain of [latex]f\left(x\right):\left[-7,\infty \right);{f}^{-1}\left(x\right)=\sqrt[\leftroot{0}\uproot{0}]{x}-7[/latex]

15. domain of [latex]f\left(x\right):\left[0,\infty \right);{f}^{-1}\left(x\right)=\sqrt[\leftroot{0}\uproot{0}]{x+5}[/latex]

17. [latex]f\left(g\left(x\right)\right)=x,g\left(f\left(x\right)\right)=x[/latex]

25. [latex]3[/latex]

27. [latex]2[/latex]

29.

33. [latex]6[/latex]

35. [latex]-4[/latex]

37. [latex]0[/latex]

39. [latex]1[/latex]

41.

[latex]x[/latex]	1	4	7	12	16
[latex]{f}^{-1}\left(x\right)[/latex]	3	6	9	13	14

45. [latex]\begin{aligned} y &= \frac{9}{5}x + 32 \ y - 32 &= \frac{9}{5}x \text{ (subtract 32 from both sides)} \ \frac{5}{9}(y - 32) &= x \text{ (multiply both sides by } \frac{5}{9}) \ f^{-1}(x) &= \frac{5}{9}(x - 32) \text{ (swap variables)} \end{aligned}[/latex]

The inverse function converts temperature from degrees Fahrenheit to degrees Celsius.